Question

【题目】如图△ABC中，BC＝3，以BC为直径的⊙O交AC于点D，若D是AC中点，∠ABC＝120°．

（1）求∠ACB的大小；

（2）求点A到直线BC的距离．

Answer 1

【答案】（1）30°；（2）.

【解析】解：（1）连接BD，

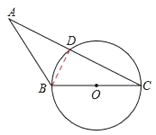
∵以BC为直径的⊙O交AC于点D，∴∠BDC=90°。

∵D是AC中点，∴BD是AC的垂直平分线。

∴AB=BC。∴∠A=∠C。

∵∠ABC=120°，∴∠A=∠C=30°。即∠ACB=30°。

（2）过点A作AE⊥BC于点E，

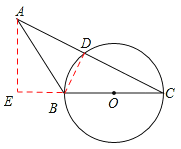
∵BC=3，∠ACB=30°，∠BDC=90°，

∴cos30°=。∴CD=。

∵AD=CD，∴AC=。

∵在Rt△AEC中，∠ACE=30°，∴。

∴点A到直线BC的距离为。

（1）根据垂直平分线的性质得出AB=BC，从而得出∠A=∠C=30°即可。

（2）根据BC=3，∠ACB=30°，∠BDC=90°，得出CD的长，从而求出AE的长度即可。