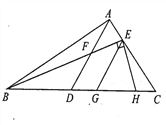
【题目】如图，在△ABC中，点D在BC 上，点E 在AC 上，AD交BE于F. 已知EG∥AD交BC于G, EH⊥BE交BC于H，∠HEG = 50°.

（1）求∠BFD的度数.

（2）若∠BAD = ∠EBC，∠C = 41°，求∠BAC的度数.

参考答案：

【答案】（1）∠BFD=40°（2）∠BAC=99°

【解析】（1）根据垂直的定义可得∠BEH=90°，然后求出∠BEG=40°，再根据两直线平行线，同位角相等可得∠BFD=∠BEG；

（2）根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BFD=∠EBC+∠ABE=∠ABC，然后根据三角形的内角和定理列式计算即可得解．

试题解析：（1）∵EH⊥BE，

∴∠BEH=90°，

∵∠HEG=50°，

∴∠BEG=40°，

又∵EG∥AD，

∴∠BFD=∠BEG=40°；

（2）∵∠BFD=∠BAD+∠ABE，∠BAD=∠EBC，

∴∠BFD=∠EBC+∠ABE=∠ABC=40°，

∵∠C=41°，

∴∠BAC=180°-∠ABC-∠C=180°-40°-41°=99°．

关闭