【题目】如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点F. 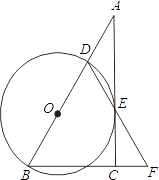
(1)求证:BD=BF;
(2)若BC=6,AD=4,求sinA的值.
参考答案:
【答案】
(1)证明:连结OE.
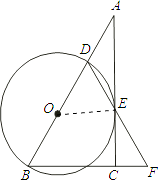
∵AC切⊙O于E,
∴OE⊥AC,
又∵∠ACB=90°即BC⊥AC,
∴OE∥BC
∴∠OED=∠F.
又∵OD=OE,
∴∠OED=∠ODE,
∴∠ODE=∠F
∴BD=BF
(2)解:设⊙O半径为r,由(1)知,OE∥BC得△AOE∽△ABC.
∴ ![]() ,即
,即 ![]() ,
,
∴r2﹣r﹣12=0,
解之得r1=4,r2=﹣3(舍去).
在Rt△AOE中,
∴sinA= ![]()
【解析】(1)利用三角形中位线定理证得OE∥BC.所以由平行线的性质、等腰三角形的性质推知∠ODE=∠F,则易证得结论;(2)设⊙O半径为r.根据相似三角形△AOE∽△ABC的对应边成比例列出关于半径r的方程,通过解方程即可求得r的值.然后通过解Rt△AOE来求sinA的值.
【考点精析】关于本题考查的切线的性质定理和相似三角形的判定与性质,需要了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.
-
科目: 来源: 题型:
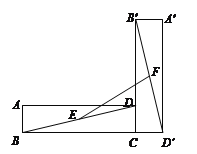
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=1,BC=7,将矩形ABCD绕点C逆时针旋转90°得到矩形A′B′CD′,点E、F分别是BD、B′D′的中点,则EF的长度为________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】铁路货运调度站有A、B两个信号灯,在灯这旁停靠着甲、乙、丙三列火车.它们中最长的车长与居中车长之差等于居中车长与最短车长之差,其中乙车的车长居中,最开始的时候,甲、丙两车车尾对齐,且车尾正好位于A信号灯处,而车头则冲着B信号灯的方向,乙车的车尾则位于B信号灯处,车头则冲着A的方向,现在,三列火车同时出发向前行驶,3秒之后三列火车的车头恰好相遇,再过9秒,甲车恰好超过丙车,而丙车也正好完全和乙车错开,请问:甲乙两车从车头相遇直到完全错开一共用了_____秒钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解全校2400名学生的阅读兴趣,从中随机抽查了部分同学,就“我最感兴趣的书籍”进行了调查:A.小说、B.散文、C.科普、D.其他(每个同学只能选择一项),进行了相关统计,整理并绘制出两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题:
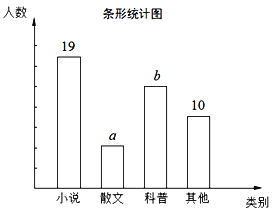

(1)本次抽查中,样本容量为______;
(2)a=______,b=______;
(3)扇形统计图中,其他类书籍所在扇形的圆心角是______°;
(4)请根据样本数据,估计全校有多少名学生对散文感兴趣.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
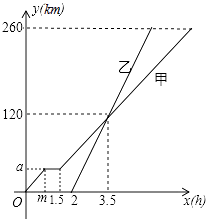
(1)求出图中m,a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车行驶多长时间时,两车恰好相距50km. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.

(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)
 (x﹣5)=3﹣
(x﹣5)=3﹣ (x﹣5)
(x﹣5)(3)
 ﹣1=
﹣1=
(4)x﹣
 (x﹣9)=
(x﹣9)= [x+
[x+ (x﹣9)]
(x﹣9)](5)
 -
- =0.5x+2
=0.5x+2
相关试题

