【题目】定义:若线段AB上有一点P,当PA=PB时,则称点P为线段AB的中点。
已知数轴上A,B两点对应数分别为a和b,![]() ,P为数轴上一动点,对应数为x.
,P为数轴上一动点,对应数为x.
(1)a=______,b=_______;
(2)若点P为线段AB的中点,则P点对应的数![]() 为______________.若B为线段AP的中点时则P点对应的数
为______________.若B为线段AP的中点时则P点对应的数![]() 为______________。
为______________。
(3)若点A、点B同时向左运动,它们的速度都为1个单位长度/秒,与此同时点P从-16处以2个单位长度/秒向右运动。
①设运动的时间为t秒,直接用含t的式子填空
AP=____________;BP=______________。
②经过多长时间后,点A、点B、点P三点中其中一点是另外两点的中点?

参考答案:
【答案】(1)-2、4;(2)1、10;(3)①-3t+14或14-3t;20-3t或3t-20;②t=![]() ,t=
,t=![]() ,t=
,t=![]() .
.
【解析】
(1)根据非负数的性质解答即可;
(2)根据线段中点的定义得出规律:若A表示的数为a,B表示的数为b,P表示的数为x,P为线段AB的中点,则2x=a+b,然后根据这个规律解答即可.
(3)①根据题意得出A、B、P表示的数,从而得出结论;
②分三种情况讨论:若P为AB的中点,若A为BP的中点,若B为AP的中点,根据(2)得出的结论列方程求解即可.
(1)根据题意得:a+2=0,b-4=0,解得:a=-2,b=4.
故答案为:-2,4.
(2)∵P为线段AB的中点,∴AP=PB,∴x-a= b-x,∴2x=a+b,∴x=![]() =
=![]() =1;
=1;
若B为线段AP的中点,则2b=a+x,解得:x=2b-a=8-(-2)=10.
故答案为:1,10.
(3)由题意得:A表示的数为:-2-t,B表示的数为:4-t,P表示的数为:-16+2t.
①AP=|(-16+2t)-(-2-t)|=|14-3t|,BP=|(-16+2t)-(4-t)|=|20-3t|,∴AP=-3t+14或14-3t;BP=20-3t或3t-20.
故答案为:-3t+14或14-3t;20-3t或3t-20.
②分三种情况讨论:
若P为AB的中点,则:2(-16+2t)=(-2-t)+(4-t),解得:t=![]() ;
;
若A为BP的中点,则:2(-2-t)=(-16+2t)+(4-t),解得:t=![]() ;
;
若B为AP的中点,则:2(4-t)=(-2-t)+(-16+2t),解得:t=![]() .
.
综上所述:t的值为![]() 或
或![]() 或
或![]() 时,点A、点B、点P三点中其中一点是另外两点的中点.
时,点A、点B、点P三点中其中一点是另外两点的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王霞和爸爸妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出坐标原点O和x轴,y轴.只知道游乐园D的坐标为(1,﹣2)
(1)请画出x轴,y轴,并标出坐标原点O.
(2)写出其他各景点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
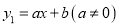 图象与反比例函数
图象与反比例函数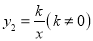 的图象交于点M、N.
的图象交于点M、N.(1)求这两个函数的表达式;
(2)根据图象写出使
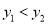 的自变量的取值范围.
的自变量的取值范围.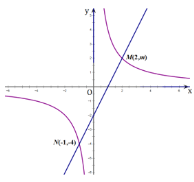
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的两个长方形用不同形式拼成图1和图2两个图形.
(1)若图1中的阴影部分面积为a2-b2;则图2中的阴影部分面积为 (用含字母a、b的代数式表示).

(2)由(1)你可以得到等式 .
(3)根据你所得到的等式解决下面的问题:
①计算:67.752-32.252;②解方程:
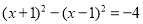
-
科目: 来源: 题型:
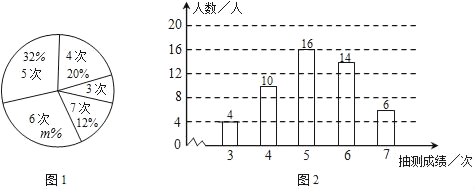
查看答案和解析>>【题目】为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制出如下的统计图①和图②,请跟进相关信息,解答下列问题:
(Ⅰ)本次抽测的男生人数为 ,图①中m的值为 ;
(Ⅱ)求本次抽测的这组数据的平均数、众数和中位数;
(Ⅲ)若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD是平行四边形,AC、BD交于点O,∠1=∠2.
(1)求证:四边形ABCD是矩形;(2)若∠BOC=120°,AB=4cm,求四边形ABCD的面积.

-
科目: 来源: 题型:
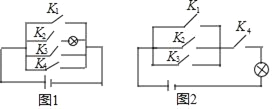
查看答案和解析>>【题目】小明学习电学知识后,用四个开关按键(每个开关键闭合的可能性相等)、一个电源和一个灯泡设计了一个电路图
(1)若小明设计的电路图(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;
(2)若小明设计的电路图(四个开关按键都处于打开状态)如图所示,求同时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)
相关试题

