【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() ,其中
,其中![]() ,
,![]() ,点
,点![]() 是
是![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 是在直线
是在直线![]() 与直线
与直线![]() 之间的一点,连接
之间的一点,连接![]() 、
、![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 交
交![]() 于
于![]() ,则
,则![]() 与
与![]() 之间可满足的数量关系式为______________.
之间可满足的数量关系式为______________.

参考答案:
【答案】![]() 或
或![]()
【解析】
分情况讨论:①点P在OB的左边时,根据三角形的内角和定理表示出∠PBO+∠POB的大小,再根据两直线平行、同旁内角互补和角平分线的定义表示出∠NBP+∠NOP,然后在△NBO中,利用三角形的内角和定理列式整理即可得到答案;
②点P在OB的右边时,求出∠CBP+∠AOP+∠BPO=360°,再根据角平分线的定义表示出∠PBN+∠PON,利用四边形的内角和定理列式整理即可得到答案.
解:①如下图,P在OB左侧时,∠BPO=2∠BNO,
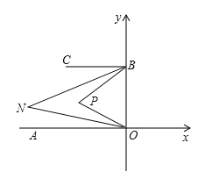
理由如下:在△BPO中,
![]()
∵BC∥OA,BN平分∠CBP,ON平分∠AOP,
∴![]() ,
,
在△NOB中,∠BNO=180°-(∠NBP+∠NOP+∠PBO+∠POB),
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ;
;
②如下图,P在OB右侧时,![]() ,理由如下:
,理由如下:
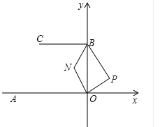
∵BC∥OA,
∴∠CBP+∠AOP+∠BPO=360°,
∵BN平分∠CBP,ON平分∠AOP,
∴![]() ,
,
∴![]() ,
,
在四边形BNOP中,
![]()
![]() ,
,
∴![]()
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解分式方程: (1)
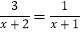 (2)
(2) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值:(2a- b)2- (a+1- b)(a+1+b)+(a+1)2,其中a=
 ,b=- 2;
,b=- 2;(2)已知x- 1=
 ,求代数式(x+1)2- 4(x+1)+4的值;
,求代数式(x+1)2- 4(x+1)+4的值;(3)先化简,再求值:2(a+
 )(a-
)(a-  )- a(a- 6)+6,其中a=
)- a(a- 6)+6,其中a= - 1.
- 1. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,若有
 条直线,则最多有______个交点;若
条直线,则最多有______个交点;若 条直线中恰好有且只有
条直线中恰好有且只有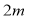 条直线互相平行,则这
条直线互相平行,则这 条直线最多有_____个交点(用含有
条直线最多有_____个交点(用含有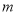 的式子表示).
的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE是∠COB的平分线,FO⊥OE,已知∠AOD=70°.
(1)求∠BOE的度数; (2)OF平分∠AOC吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于数对(a,b)、(c,d),定义:当且仅当a=c且b=d时,(a,b)=(c,d);并定义其运算如下: (a,b)※(c,d)=(ac﹣bd,ad+bc),如(1,2)※(3,4)=(1×3﹣2×4,1×4+2×3)=(﹣5,10).若(x,y)※(1,﹣1)=(1,3),则xy的值是( )
A.﹣1
B.0
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

相关试题

