【题目】有这样一个问题:探究函数y= ![]() 的图象与性质,小静根据学习函数的经验,对函数y=
的图象与性质,小静根据学习函数的经验,对函数y= ![]() 的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
的图象与性质进行了探究,下面是小静的探究过程,请补充完整: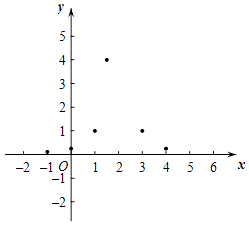
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下表是y与x的几组对应值.
x | … | ﹣1 | 0 | 1 |
|
| 3 | 4 | … |
y | … |
|
| 1 | 4 | m | 1 |
| … |
表中的m=;
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
(4)结合函数图象,写出一条该函数图象的性质: .
参考答案:
【答案】
(1)x≠2
(2)4
(3)解:如下图所示:
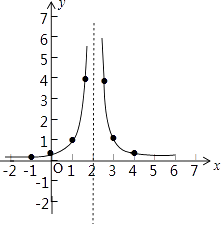
(4)函数图象关于直线x=2对称
【解析】解:(1)函数y= ![]() 的自变量x的取值范围是x﹣2≠0,即x≠2,
的自变量x的取值范围是x﹣2≠0,即x≠2,
所以答案是:x≠2;
⑵由表可知当x=0和x=4、x=1和x=3时,函数值y均相等,
∴当x= ![]() 和x=
和x= ![]() 时,函数值相等,为4,即m=4,
时,函数值相等,为4,即m=4,
所以答案是:4;
⑷由图象可知,函数图象关于直线x=2对称,
所以答案是:函数图象关于直线x=2对称.
【考点精析】本题主要考查了函数自变量的取值范围和函数的图象的相关知识点,需要掌握使函数有意义的自变量的取值的全体,叫做自变量的取值范围;函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.

(1)求证:BC是⊙O的切线;
(2)当点E为弧AD的中点且∠BED=30°时,⊙O半径为2,求DF的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】中央电视台举办的“中国汉字听写大会”节目受到中学生的广泛关注.某中学为了了解学生对观看“中国汉字听写大会”节目的喜爱程度,对该校部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图.在条形图中,从左向右依次为A类(非常喜欢),B类(较喜欢),C类(一般),D类(不喜欢).已知A类和B类所占人数的比是5:9,请结合两幅统计图,回答下列问题:
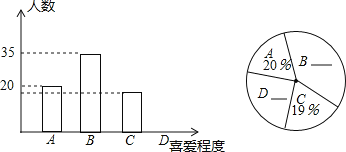
(1)写出本次抽样调查的样本容量;
(2)请补全两幅统计图;
(3)若该校有2000名学生.请你估计观看“中国汉字听写大会”节目不喜欢的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt ABC中,
 ,AB=5cm, AC=3cm, 动点P从点B出发沿射线BC以2cm/s 的速度移动,设运动的时间为t秒.t= __________ 时三角形ABP为直角三角形.
,AB=5cm, AC=3cm, 动点P从点B出发沿射线BC以2cm/s 的速度移动,设运动的时间为t秒.t= __________ 时三角形ABP为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣4mx(m≠0)与x轴交于A,B两点(点A在点B的左侧).
(1)求点A,B的坐标及抛物线的对称轴;
(2)过点B的直线l与y轴交于点C,且tan∠ACB=2,直接写出直线l的表达式;
(3)如果点P(x1 , n)和点Q(x2 , n)在函数y=mx2﹣4mx(m≠0)的图象上,PQ=2a且x1>x2 , 求x12+ax2﹣6a+2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E为AB边上一点,连接DE,将△ADE绕点D逆时针旋转90°得到△CDF,作点F关于CD的对称点,记为点G,连接DG.

(1)依题意在图1中补全图形;
(2)连接BD,EG,判断BD与EG的位置关系并在图2中加以证明;
(3)当点E为线段AB的中点时,直接写出∠EDG的正切值.
相关试题

