【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

参考答案:
【答案】(1)ECF=![]() ;
;
(2)证明见解析;
(3)结论:当O=60时 ,CD平分OCF,理由见解析.
【解析】试题分析:由两直线平行,同位角相等得∠ACE =40,由平角定义得∠ACD=![]() ,再由角平分线定义得
,再由角平分线定义得![]() ,由邻补角定义得到ECF=
,由邻补角定义得到ECF=![]() ;(2)由垂直的定义得
;(2)由垂直的定义得![]() ,由
,由![]() 得
得![]() ,由等角的余角相等可证;(3)由两直线平行,同位角相等得∠DCO=∠O=60,由角平分线性质得∠DCF=60,由等量代换得
,由等角的余角相等可证;(3)由两直线平行,同位角相等得∠DCO=∠O=60,由角平分线性质得∠DCF=60,由等量代换得![]() 即可得证.
即可得证.
试题解析:(1)∵DE//OB ,
∴∠O=∠ACE,(两直线平行,同位角相等)
∵O =40,
∴∠ACE =40,
∵∠ACD+∠ACE=![]() (平角定义)
(平角定义)
∴ ∠ACD=![]()
又 ∵CF平分ACD ,
∴![]() (角平分线定义)
(角平分线定义)
∴ ECF=![]()
(2)证明:∵CG CF,
∴![]() .
.
∴![]()
又 ∵![]()
![]() )
)
∴![]()
∵![]()
∴![]() (等角的余角相等)
(等角的余角相等)
即CG平分OCD .
(3)结论:当O=60时 ,CD平分OCF .
当O=60时
∵DE//OB,
∴ ∠DCO=∠O=60.
∴ ∠ACD=120.
又 ∵CF平分ACD
∴ ∠DCF=60,
∴![]()
即CD平分OCF .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( ).
A. “打开电视,正在播放《新闻联播》”是必然事件
B. 一组数据的波动越大,方差越小
C. 数据1,1,2,2,3的众数是3
D. 想了解某种饮料中含色素的情况,宜采用抽样调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC⊥CB,垂足为C点,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC方向匀速移动.点P的运动速度为2cm/s.设动点P运动的时间为ts.为方便说明,我们分别记三角形ABC面积为S,三角形PCQ的面积为S1,三角形PAQ的面积为S2,三角形ABP的面积为S3.
(1)S3= cm2(用含t的代数式表示);
(2)当点P运动几秒,S1=
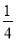 S,说明理由;
S,说明理由;(3)请你探索是否存在某一时刻,使得S1=S2=S3?若存在,求出t值;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,B1(0,1),B2(0,3),B3(0,6),B4(0,10),…,以B1B2为对角线作第一个正方形A1B1C1B2,以B2B3为对角线作第二个正方形A2B2C2B3,以B3B4为对角线作第三个正方形A3B3C3B4,…,如果所作正方形的对角线BnBn+1都在y轴上,且BnBn+1的长度依次增加1个单位,顶点An都在第一象限内(n≥1,且n为整数). 那么A1的坐标为____________;An的坐标为_________(用含n的代数式表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:
①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某地区,高度每升高100米,气温下降0.8 ℃.若在该地区的山脚测得气温为15 ℃,在山顶测得气温为-5 ℃,你能求出从山顶到山脚的高度吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某初中毕业班的每一个同学都将自己的相片向全班其他同学各送一张表示留念,全班共送了2550张相片,如果全班有x名学生,根据题意,列出方程为( )
A. x(x+1)=2550 B. x(x﹣1)=2550 C. 2x(x+1)=2550 D. x(x﹣1)=2550×2
相关试题

