【题目】如图,在正方形ABCD中,E为AB边上一点,连接DE,将△ADE绕点D逆时针旋转90°得到△CDF,作点F关于CD的对称点,记为点G,连接DG.
(1)依题意在图1中补全图形;
(2)连接BD,EG,判断BD与EG的位置关系并在图2中加以证明;
(3)当点E为线段AB的中点时,直接写出∠EDG的正切值.
参考答案:
【答案】
(1)解:如图所示:
依题意补全图形如图1:
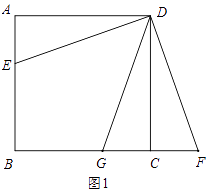
(2)解:结论:BD⊥EG.
证明:如图2,BD,EG交于M,
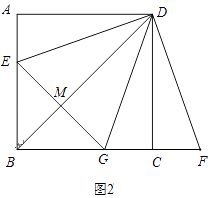
∵正方形ABCD,
∴AB=BC,∠DAE=∠DCB=90°,
由旋转可得△ADE≌△CDF,DE=DF,AE=CF
∴∠DCF=∠DAE=∠DCB=90°,
∴点B,C,F在一条直线上.
∵点G与点F关于CD的对称
∴△DCG≌△DCF,DG=DF,CG=CF
∴DE=DG,AE=CG,
∴BE=BG
∴BD⊥EG于M.
(3)解:如图3,过G作GM⊥DE于M,

由(2)知,DE=DG,
设BE=x,
∴AE=CF=CG=BG=x,
∴AD=2x,
在Rt△ADE中,DE= ![]() =
= ![]() x,
x,
∴DG= ![]() x,
x,
在Rt△BEG中,EG= ![]() x,
x,
设DM=a,
∴EM=DE﹣DM= ![]() x﹣a,
x﹣a,
在Rt△EMG中,MG2=EG2﹣EM2,
∴MG2=2x2﹣( ![]() x﹣a)2,
x﹣a)2,
在Rt△DMG中,MG2=5x2﹣a2,
∴2x2﹣( ![]() x﹣a)2=5x2﹣a2,
x﹣a)2=5x2﹣a2,
∴a= ![]() ,
,
∴MG= ![]() x
x
在Rt△DMG中,tan∠EDG= ![]() =
= ![]() .
.
即:∠EDG的正切值为 ![]() .
.
【解析】(1)根据旋转中心旋转方向旋转角度画出图形即可;(2)先利用旋转判断出B、C、F在一条直线上,进而利用轴对称得出△DCG≌△DCF即可;(3)过G作GM⊥DE于M,构造出直角三角形,再利用勾股定理即可表示出GM、DM即可得出结论。
【考点精析】利用勾股定理的概念和正方形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数y=
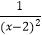 的图象与性质,小静根据学习函数的经验,对函数y=
的图象与性质,小静根据学习函数的经验,对函数y= 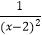 的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
的图象与性质进行了探究,下面是小静的探究过程,请补充完整: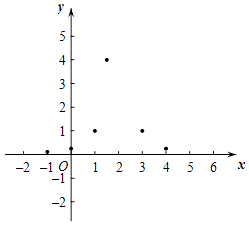
(1)函数y=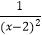 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下表是y与x的几组对应值.x
…
﹣1
0
1


3
4
…
y
…


1
4
m
1

…
表中的m=;
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
(4)结合函数图象,写出一条该函数图象的性质: . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣4mx(m≠0)与x轴交于A,B两点(点A在点B的左侧).
(1)求点A,B的坐标及抛物线的对称轴;
(2)过点B的直线l与y轴交于点C,且tan∠ACB=2,直接写出直线l的表达式;
(3)如果点P(x1 , n)和点Q(x2 , n)在函数y=mx2﹣4mx(m≠0)的图象上,PQ=2a且x1>x2 , 求x12+ax2﹣6a+2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,给出如下定义:
对于⊙C及⊙C外一点P,M,N是⊙C上两点,当∠MPN最大时,称∠MPN为点P关于⊙C的“视角”.
(1)如图,⊙O的半径为1,
①已知点A(0,2),画出点A关于⊙O的“视角”;若点P在直线x=2上,则点P关于⊙O的最大“视角”的度数 ;
(2)在第一象限内有一点B(m,m),点B关于⊙O的“视角”为60°,求点B的坐标.
(3)若点P在直线y=﹣ x+2上,且点P关于⊙O的“视角”大于60°,求点P的横坐标xP的取值范围.
x+2上,且点P关于⊙O的“视角”大于60°,求点P的横坐标xP的取值范围.
(4)⊙C的圆心在x轴上,半径为1,点E的坐标为(0,1),点F的坐标为(0,﹣1),若线段EF上所有的点关于⊙C的“视角”都小于120°,直接写出点C的横坐标xC的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的解析式;
(2)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

相关试题

