【题目】如图,在等腰梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6Cm,点P从A开始沿AB边向B以每秒3cm的速度移动,点Q从C开始沿CD边向D以每秒1cm的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达终点时,运动停止,设运动时间为![]() 秒.
秒.
(1)求证:当![]() 时,四边形APQD是平行四边形;
时,四边形APQD是平行四边形;
(2)PQ是否可能平分对角线BD?若能,求出当![]() 为何值时PQ平分BD;若不能,请说明理由;
为何值时PQ平分BD;若不能,请说明理由;
(3)当PD=PQ时,求![]() 的值.
的值.

参考答案:
【答案】(1)证明见解析;(2)当t=3秒时,PQ平分对角线BD.(3)若△DPQ是以PQ为腰的等腰三角形,t的值为![]() .
.
【解析】
(1)由题意可得当t=4秒时,两点停止运动,在运动过程中AP=3t,CQ=t,即可得BP=12-3t,DQ=6-t,由t=![]() ,即可求得AP=DQ,又由AP∥DQ,即可判定四边形APQD是平行四边形;
,即可求得AP=DQ,又由AP∥DQ,即可判定四边形APQD是平行四边形;
(2)首先连接BD交PQ于点E,若PQ平分对角线BD,则DE=BE,易证得△DEQ≌△BEP,继而可得四边形DPBQ为平行四边形,则可得6-t=12-3t,解此方程即可求得答案.
(3)分两种情况:①当PQ=PD时,作DN⊥AB于N,QM⊥AB于M,CE⊥AB与E,如图所示:则DN=QM,AN=BE=![]() (AB-CD)=3,ME=CQ=t,得出PN=AP-AN=3t-3,PM=BP-BE-ME=9-4t,由PN=PM得出方程,解方程即可;
(AB-CD)=3,ME=CQ=t,得出PN=AP-AN=3t-3,PM=BP-BE-ME=9-4t,由PN=PM得出方程,解方程即可;
②当PQ=DQ=6-t时,由勾股定理得出方程,方程无解;即可得出答案.
(1)证明:∵![]() <
<![]() ,
,
∴当t=4秒时,两点停止运动,在运动过程中AP=3t,CQ=t,
∴BP=12-3t,DQ=6-t,
当t=![]() 时,DQ=6-
时,DQ=6-![]() =
=![]() ,AP=3×
,AP=3×![]() =
=![]() ,
,
∴AP=DQ
又∵四边形ABCD为等腰梯形,
∴AP∥DQ,
∴四边形APQD为平行四边形;
(2)解:PQ能平分对角线BD,当t=3秒时,PQ平分对角线BD.
理由如下:
连接BD交PQ于点E,如图1所示:
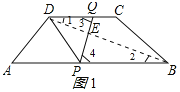
若PQ平分对角线BD,则DE=BE,
∵CD∥AB,
∴∠1=∠2,∠3=∠4,
在△DEQ和△BEP中,
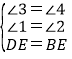 ,
,
∴△DEQ≌△BEP(AAS),
∴DQ=BP,
即四边形DPBQ为平行四边形,
∴6-t=12-3t,
解得t=3,符合题意,
∴当t=3秒时,PQ平分对角线BD.
(3)解:分两种情况:
①当PQ=PD时,作DN⊥AB于N,QM⊥AB于M,CE⊥AB与E,如图2所示:
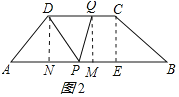
则DN=QM,AN=BE=![]() (AB-CD)=3,ME=CQ=t,
(AB-CD)=3,ME=CQ=t,
∴PN=AP-AN=3t-3,PM=BP-BE-ME=9-4t,
∵PQ=PD,
∴PN=PM,
∴3t-3=9-4t,
解得:t=![]() ;
;
②当PQ=DQ=6-t时,由勾股定理得:PQ2=QM2+PM2=42+(9-4t)2,
∴42+(9-4t)2=(6-t)2,
整理得:15t2-60t+61=0,
解得△<0,方程无解;
综上所述:若△DPQ是以PQ为腰的等腰三角形,t的值为![]() .
.
-
科目: 来源: 题型:
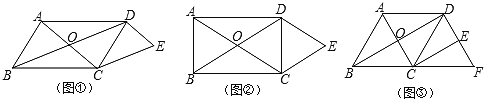
查看答案和解析>>【题目】(1)发现问题:如图①平行四边形AB、CD的对角线相交于点O,DE∥AC,CE∥BD,可知:四边形OCED是什么形(不需要证明).
(2)类比探究:如图②矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD,四边形OCED是什么形,请说明理由;
(3)拓展应用:如图③,菱形ABCD的对角线相交于点O,∠ABC=60°,BC=4,DE∥AC交BC的延长线于点F,CE∥BD求四边形ABFD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:计算与化简
(1)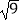 ﹣(﹣2)2+(﹣0.1)0;
﹣(﹣2)2+(﹣0.1)0;
(2)(x﹣2)2﹣(x+3)(x﹣1). -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进甲,乙两种服装后,都加价50%标价出售.春节期间,商场搞优惠促销,决定将甲,乙两种服装分别按标价的七折和八折出售.某顾客购买甲,乙两种服装共付款186元,两种服装标价和为240元.问:这两种服装打折之后售出的利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某加工厂加工一批绿色蔬菜,若12个大加工车间和15个小加工车间一天同时加工,则可加工绿色蔬菜1575吨;若3个大加工车间和5个小加工车间一天同时加工,则可加工绿色蔬菜450吨.
(1)每个大车间和每个小车间每天各加工多少吨绿色蔬菜?
(2)若该工厂有25个大加工车间,20个小加工车间;每个大车间每天耗费3000元,每个小车间每天耗费2500元,现有2250吨绿色蔬菜,要求一天之内加工完,如何分配车间才能更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点P是AB的中点,
 的延长线于点E,连接AE,过点A作
的延长线于点E,连接AE,过点A作 交DP于点F,连接BF、
交DP于点F,连接BF、 下列结论中:
下列结论中: ≌
≌ ;
; ;
; 是等边三角形;
是等边三角形; ;
; 其中正确的是
其中正确的是


A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数( )

A. 24°B. 25°C. 30°D. 35°
相关试题

