【题目】如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间________秒时,以点P,Q,E,D为顶点的四边形是平行四边形.

参考答案:
【答案】2或 ![]()
【解析】
由已知以点P,Q,E,D为顶点的四边形是平行四边形有两种情况,(1)当Q运动到E和B之间,(2)当Q运动到E和C之间,根据平行四边形的判定,由AD∥BC,所以当PD=QE时为平行四边形.据此设运动时间为t,列出关于t的方程求解.
由已知梯形,
当Q运动到E和B之间,设运动时间为t,则得:![]() =6-t,
=6-t,
解得:t=![]() ,
,
当Q运动到E和C之间,设运动时间为t,则得:![]() -2t=6-t,
-2t=6-t,
解得:t=2,
故当运动时间t为2或![]() 秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
故答案为:2或 ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));正方形A2B2C2D2的面积为________,以此下去…,则正方形AnBnCnDn的面积为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空,如图:方格纸中每个小正方形的边长都为 1,
 的顶点都在方格纸的格点上,
的顶点都在方格纸的格点上,将
 经过一次平移后得到
经过一次平移后得到 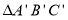 .图中标 出了点
.图中标 出了点  的对应点
的对应点  .
.(1)请画出平移后的
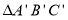 ;
;(2)若连接
 ,
,  ,则这两条线段的关系是_____;
,则这两条线段的关系是_____;(3)利用网格画出
 中
中  边上的中线
边上的中线  以及
以及 边上的高
边上的高  ;
;(4)线段
 在平移过程中扫过区域的面积为 _____.
在平移过程中扫过区域的面积为 _____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数。
例如,
 展开式中的系数1、2、1恰好对应图中第三行的数字;
展开式中的系数1、2、1恰好对应图中第三行的数字;再如,
 展开式中的系数1、3、3、1恰好对应图中第四行的数字。
展开式中的系数1、3、3、1恰好对应图中第四行的数字。请认真观察此图,写出(a+b)4的展开式,(a+b)4=_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径为
 ,点
,点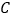 在圆周上(异于
在圆周上(异于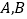 ),
),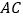 是
是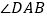 的平分线,
的平分线,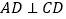 .
.(1)求证:直线
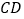 是⊙O的切线;
是⊙O的切线;(2)若
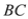 =3,
=3,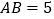 ,求
,求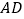 的值.
的值.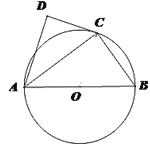
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级2班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):

(l)甲队成绩的中位数是____分,乙队成绩的众数是____分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队的平均成绩是9分,方差是1.4分,则成绩较为整齐的是哪个队?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一方有难八方支援,某市政府筹集抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型可供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车来运送,需运费8200元,则分别需甲、乙两种车各几辆?
(2)为了节约运费,该市政府共调用16辆甲、乙,丙三种车都参与运送物资,试求出有几种运送方案,哪种方案的运费最省?其费用是多少元?
相关试题

