【题目】某商场用2730元购进A、B两种新型节能日光灯共60盏,这两种日光灯的进价、标价如下表所示.
价格/类型 | A型 | B型 |
进价(元/盏) | 35 | 65 |
标价(元/盏) | 50 | 100 |
(1)这两种日光灯各购进多少盏?
(2)若A型日光灯按标价的9折出售,要使这批日光灯全部售出后商场获得810元的利润,则B型日光灯应按标价的几折出售?
参考答案:
【答案】(1)购进A型日光灯39盏,购进B型日光灯21盏.(2)B型日光灯应按标价的八五折出售.
【解析】
(1)设购进A型日光灯x盏,则购进B型日光灯(60﹣x)盏,则购买A型灯钱数+购买B型灯钱数=2730,据此列出方程,解方程即可;
(2)根据利润=售价-进价,知商场共获利=A型灯利润+B型灯利润,设B型日光灯应按标价的a折出售,列方程求解即可.
(1)设购进A型日光灯x盏,则购进B型日光灯(60﹣x)盏,
根据题意得:35x+65(60﹣x)=2730,
解得:x=39,
∴60﹣x=21,
答:购进A型日光灯39盏,购进B型日光灯21盏;
(2)设B型日光灯应按标价的a折出售,
根据题意得:(50×0.9﹣35)×39+(100×![]() ﹣65)×21=810,
﹣65)×21=810,
解得:a=8.5,
答:B型日光灯应按标价的八五折出售.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
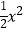 +bx+c图象经过A(﹣1,0),B(4,0)两点.
+bx+c图象经过A(﹣1,0),B(4,0)两点.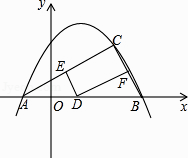
(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE//BC交AC于E,DF//AC交BC于F.
①求证:四边形DECF是矩形;
②试探究:在点D运动过程中,DE、DF、CF的长度之和是否发生变化?若不变,求出它的值,若变化,试说明变化情况. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l:y=﹣
 x+b与x轴,y轴的交点分别为A,B,直线l1:y=
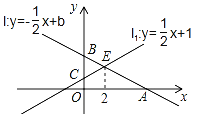
x+b与x轴,y轴的交点分别为A,B,直线l1:y= x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为2.
x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为2.(1)求实数b的值和点A的坐标;
(2)设点D(a,0)为x轴上的动点,过点D作x轴的垂线,分别交直线l与直线ll于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.
-
科目: 来源: 题型:
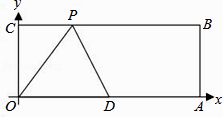
查看答案和解析>>【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)先化简,再求值:1﹣ ]÷
]÷  +
+  ,其中a=
,其中a=  .
.
(2)解不等式组: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x(x大于0)秒.
(1)点C表示的数是 ;
(2)当x= 秒时,点P到达点A处?
(3)运动过程中点P表示的数是 (用含字母x的式子表示);
(4)当P,C之间的距离为2个单位长度时,求x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小兵、小颖三人的家和学校在同一条东西走向的路上,星期天,老师到这三家进行家访,从学校出发先向东走 250m 到小明家,后又向东走 350m 到小兵家,再向西行 800m 到小颖家,最后回到学校.
(1)以学校为原点,画出数轴并在数轴上分别表示出小明、小兵、小颖家的位置;
(2)小明家距离小颖家多远?
(3)这次家访,老师共走了多少千米的路程?
相关试题

