【题目】(10分)(1)【问题发现】小明遇到这样一个问题:
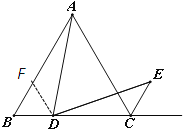
如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.
(1)小明发现,过点D作DF//AC,交AC于点F,通过构造全等三角形,经过推理论证,能够使问题得到解决,请直接写出AD与DE的数量关系: ;
(2)【类比探究】如图2,当点D是线段BC上(除B,C外)任意一点时(其它条件
不变),试猜想AD与DE之间的数量关系,并证明你的结论.
(3)【拓展应用】当点D在线段BC的延长线上,且满足CD=BC(其它条件不变)时,
请直接写出△ABC与△ADE的面积之比.

参考答案:
【答案】(1)AD=DE;(2)AD=DE,证明见解析;(3)![]() .
.
【解析】
试题分析:本题难度中等。主要考查学生对探究例子中的信息进行归纳总结。并能够结合三角形的性质是解题关键。
试题解析:(10分)
(1)AD=DE.
(2)AD=DE.
证明:如图2,过点D作DF//AC,交AC于点F,
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=∠ABC=60°.
又∵DF//AC,
∴∠BDF=∠BFD=60°
∴△BDF是等边三角形,BF=BD,∠BFD=60°,
∴AF=CD,∠AFD=120°.
∵EC是外角的平分线,
∠DCE=120°=∠AFD.
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠FAD=60°+∠FAD.
∵∠ADC=∠ADE+∠EDC=60°+∠EDC,
∴∠FAD=∠EDC.
∴△AFD≌△DCE(ASA),
∴AD=DE;
(3)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,在边长为1的正方形网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,1),B(2,3).
(1)请在图中画出△AOB关于y轴的对称△A′OB′,点A′的坐标为 ,点B′的坐标为 ;
(2)请写出A′点关于x轴的对称点A′'的坐标为 ;
(3)求△A′OB′的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】实践与探究:已知AB∥CD,点P是平面内一点.
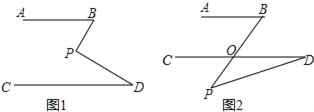
(1)如图1,若点P在AB、CD内部,请探究∠BPD、∠B、∠D之间有何数量关系?请证明你的结论.
(2)如图2,若点P移动到AB、CD外部,那么∠BPD、∠B、∠D之间的数量关系是否发生变化?请给出你的证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,E是△ABD内的点,EB=EC.
(1)如图1,若EB=BC,求∠EBD的度数;
(2)如图2,EC与BD交于点F,连接AE,若
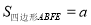 ,试探究线段FC与BE之间的等量关系,并说明理由.
,试探究线段FC与BE之间的等量关系,并说明理由.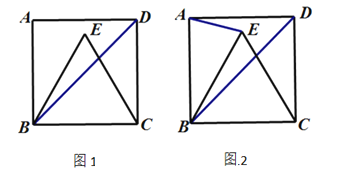
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条笔直跑道上的A,B两处相距500米,甲从A处,乙从B处,两人同时相向匀速而跑,直到乙到达A处时停止,且甲的速度比乙大.甲、乙到A处的距离
 (米)与跑动时间
(米)与跑动时间 (秒)的函数关系如图14所示.
(秒)的函数关系如图14所示.(1)若点M的坐标(100,0),求乙从B处跑到A处的过程中
 与
与 的函数解析式;
的函数解析式;(2)若两人之间的距离不超过200米的时间持续了40秒.
①当
 时,两人相距200米,请在图14中画出P(
时,两人相距200米,请在图14中画出P( ,0).保留画图痕迹,并写出画图步骤;
,0).保留画图痕迹,并写出画图步骤;②请判断起跑后
 分钟,两人之间的距离能否超过420米,并说明理由.
分钟,两人之间的距离能否超过420米,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某山区有若干名中、小学生因贫困失学需要捐助,资助一名中学生的学习费用需要a元,资助一名小学生的学习费用需要b元.某校学生积极捐款,初中各年级学生捐款数额与其捐助贫困中学生和小学生人数的部分情况如下表:
捐款数额/元
资助贫困中学生人数/名
资助贫困小学生人数/名
七年级
4000
2
4
八年级
4200
3
3
九年级
5000
(1)求a,b的值;
(2)九年级学生的捐款恰好解决了剩余贫困中小学生的学习费用,请计算九年级学生可捐助的贫困小学生人数.
相关试题

