【题目】实践与探究:已知AB∥CD,点P是平面内一点.
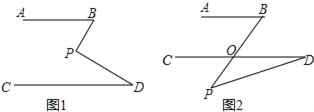
(1)如图1,若点P在AB、CD内部,请探究∠BPD、∠B、∠D之间有何数量关系?请证明你的结论.
(2)如图2,若点P移动到AB、CD外部,那么∠BPD、∠B、∠D之间的数量关系是否发生变化?请给出你的证明.
参考答案:
【答案】(1)∠BPD=∠B+∠D,证明见解析;(2)发生变化,应该为∠BPD=∠B﹣∠D,证明见解析.
【解析】
试题(1)作PQ∥AB,根据平行线的性质即可得∠BPD=∠B+∠D;
(2)作PE∥CD,根据平行线的性质即可得∠BPD=∠B-∠D;
试题解析:(1)∠BPD=∠B+∠D,证明如下:
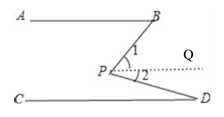
作PQ∥AB,如图,
∵AB∥CD,∴AB∥PQ∥CD,∴∠1=∠B,∠2=∠D,∴∠BPD=∠B+∠D .
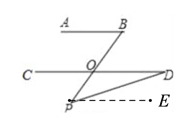
(2)发生变化,应该为∠BPD=∠B﹣∠D,证明如下:
过P做PE∥CD,∵AB∥CD,PE∥CD,∴ AB∥CE ,∴∠B=∠EPB, ∠D=∠EPD,而∠B=∠BPD+∠DPE,
∴∠B=∠BPD+∠D,即∠BPD=∠B﹣∠D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,在边长为1的正方形网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,1),B(2,3).
(1)请在图中画出△AOB关于y轴的对称△A′OB′,点A′的坐标为 ,点B′的坐标为 ;
(2)请写出A′点关于x轴的对称点A′'的坐标为 ;
(3)求△A′OB′的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)(1)【问题发现】小明遇到这样一个问题:
如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.
(1)小明发现,过点D作DF//AC,交AC于点F,通过构造全等三角形,经过推理论证,能够使问题得到解决,请直接写出AD与DE的数量关系: ;
(2)【类比探究】如图2,当点D是线段BC上(除B,C外)任意一点时(其它条件
不变),试猜想AD与DE之间的数量关系,并证明你的结论.
(3)【拓展应用】当点D在线段BC的延长线上,且满足CD=BC(其它条件不变)时,
请直接写出△ABC与△ADE的面积之比.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,E是△ABD内的点,EB=EC.
(1)如图1,若EB=BC,求∠EBD的度数;
(2)如图2,EC与BD交于点F,连接AE,若
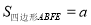 ,试探究线段FC与BE之间的等量关系,并说明理由.
,试探究线段FC与BE之间的等量关系,并说明理由.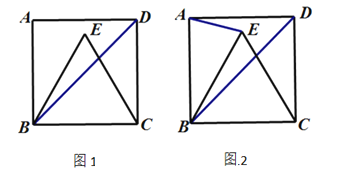
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条笔直跑道上的A,B两处相距500米,甲从A处,乙从B处,两人同时相向匀速而跑,直到乙到达A处时停止,且甲的速度比乙大.甲、乙到A处的距离
 (米)与跑动时间
(米)与跑动时间 (秒)的函数关系如图14所示.
(秒)的函数关系如图14所示.(1)若点M的坐标(100,0),求乙从B处跑到A处的过程中
 与
与 的函数解析式;
的函数解析式;(2)若两人之间的距离不超过200米的时间持续了40秒.
①当
 时,两人相距200米,请在图14中画出P(
时,两人相距200米,请在图14中画出P( ,0).保留画图痕迹,并写出画图步骤;
,0).保留画图痕迹,并写出画图步骤;②请判断起跑后
 分钟,两人之间的距离能否超过420米,并说明理由.
分钟,两人之间的距离能否超过420米,并说明理由.
相关试题

