【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF. 
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
参考答案:
【答案】
(1)解:平行;
证明:∵∠2+∠CDB=180°,∠1+∠2=180°,
∴∠CDB=∠1,
∴AE∥FC
(2)解:平行,
证明:∵AE∥FC,
∴∠CDA+∠DAE=180°,
∵∠DAE=∠BCF
∴∠CDA+∠BCF=180°,
∴AD∥BC
(3)解:平分,
证明:∵AE∥FC,
∴∠EBC=∠BCF,
∵AD∥BC,
∴∠BCF=∠FDA,∠DBC=∠BDA,
又∵DA平分∠BDF,即∠FDA=∠BDA,
∴∠EBC=∠DBC,
∴BC平分∠DBE.
【解析】(1)∠1+∠2=180°而∠2+∠CDB=180°,则∠CDB=∠1,根据同位角相等,两直线平行,求得结论;(2)要说明AD与BC平行,只要说明∠BCF+∠CDA=180°即可.而根据AE∥FC可得:∠CDA+∠DEA=180°,再据∠DAE=∠BCF就可以证得.(3)BC平分∠DBE即说明∠EBC=∠DBC是否成立.根据AE∥FC,可得:∠EBC=∠BCF,据AD∥BC得到:∠BCF=∠FAD,∠DBC=∠BAD,进而就可以证出结论.
【考点精析】根据题目的已知条件,利用平行线的判定的相关知识可以得到问题的答案,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】x的2倍与3的差不小于1,列出不等式是( )
A. 2x-3≤1 B. 2x-3≥1
C. 2x-3<1 D. 2x-3>1
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)解方程:(x+1)2=64;
(2)计算:(﹣2)3×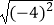 +
+ 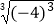 ×(
×(  )2﹣
)2﹣ 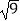 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a﹣7的平方根是±5,2a+b﹣1的算术平方根是4,求﹣
 +b的值.
+b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系xOy中,二次函数y=﹣x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C.
(1)求这个二次函数的解析式并写出其图象顶点D的坐标;
(2)求∠CAD的正弦值;
(3)设点P在线段DC的延长线上,且∠PAO=∠CAD,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2+kx﹣3=0有一个根为1,则k的值为( )
A.﹣2B.2C.﹣4D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地2018年4月某天的最高气温为8 ℃,则这天的气温t(℃)用不等式表示为________,11月某天的最低气温为-2 ℃,则这天的气温t(℃)用不等式表示为________.
相关试题

