【题目】下列说法中,正确的个数有( )
①已知直角三角形的面积为2,两直角边的比为1:2,则斜边长为![]() ;
;
②直角三角形的最大边长为![]() ,最短边长为1,则另一边长为
,最短边长为1,则另一边长为![]() ;
;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;
④等腰三角形面积为12,底边上的高为4,则腰长为5.
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】
根据勾股定理以及三角形的内角和定理一一判断解答即可.
解:①设较短的一个直角边为M,则另一个直角边为2M,所以![]() M
M![]() 2M=2,解得M=
2M=2,解得M=![]() ,2M=2
,2M=2![]() .根据勾股定理解得斜边为
.根据勾股定理解得斜边为![]() .所以此项正确;
.所以此项正确;
②根据勾股定理解得,另一边=![]() =
=![]() ,所以此项正确;
,所以此项正确;
③设∠A=x,则∠B=5x,∠C=6x.因为x+5x+6x=180![]() 解得x=15
解得x=15![]() ,从而得到三个角分别为15
,从而得到三个角分别为15![]() ,75
,75![]() ,90
,90![]() .即△ABC为直角三角形,所以此项正确;
.即△ABC为直角三角形,所以此项正确;
④已知面积和高则可以得到底边为6,又因为是等腰三角形,则底边上的高也是底边上的中线,则可以得到底边的一半为3.此时再利用勾股定理求得腰长为![]() =5.所以此项正确.
=5.所以此项正确.
所以正确的有四个.
所以D选项是正确的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中五次行驶纪录如下。(单位:千米)
第一次
第二次
第三次
第四次
第五次
-4
+7
-9
+7
-2
(1)求第二次记录时距A地多远?
(2)在第______次纪录时距A地最远。
(3)若每千米耗油0.8升,问共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的关系是___;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某兴趣小组用高为1.6米的仪器测量塔CD的高度.由距塔CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α.测得A,B之间的距离为10米,tanα=1.6,tanβ=1.2,试求塔CD的大约高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有四个三角形,分别满足下列条件:(1)一个角等于另外两个内角之和;(2)三个内角之比为3:4:5;(3)三边之比为5:12:13;(4)三边长分别为5,24,25.其中直角三角形有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为正数,满足如下两个条件:a+b+c=32 ①
 ② 是否存在以
② 是否存在以  为三边长的三角形?如果存在,求出三角形的最大内角.
为三边长的三角形?如果存在,求出三角形的最大内角. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的点A、B、C分别表示数﹣3、﹣1、2.
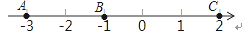
(1)A、B两点的距离AB=________,A、C两点的距离AC=________ ;
(2)通过观察,可以发现数轴上两点间距离与这两点表示的数的差的绝对值有一定关系,按照此关系,若点E表示的数为x,则AE=________ ;
(3)利用数轴直接写出|x﹣1|+|x+3|的最小值=________ .
相关试题

