【题目】已知抛物线与x轴交于A(6,0)、B(![]() ,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
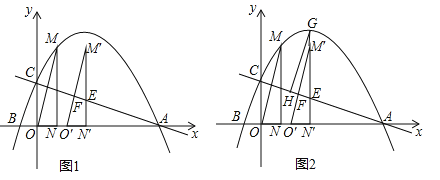
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)①1;②t=2时,EH最大值为
;(2)①1;②t=2时,EH最大值为![]() .
.
【解析】
试题分析:(1)设抛物线解析式为![]() ,把点M(1,3)代入即可求出a,进而解决问题.
,把点M(1,3)代入即可求出a,进而解决问题.
(2))①如图1中,AC与OM交于点G.连接EO′,首先证明△AOC∽△MNO,推出OM⊥AC,在RT△EO′M′中,利用勾股定理列出方程即可解决问题.
②由△GHE∽△AOC得![]() =
=![]() =
=![]() ,所以EG最大时,EH最大,构建二次函数求出EG的最大值即可解决问题.
,所以EG最大时,EH最大,构建二次函数求出EG的最大值即可解决问题.
试题解析:(1)设抛物线解析式为![]() ,把点M(1,3)代入得a=
,把点M(1,3)代入得a=![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ,∴
,∴![]() .
.
(2)①如图1中,AC与OM交于点G.连接EO′.∵AO=6,OC=2,MN=3,ON=1,∴![]() =3,∴
=3,∴![]() ,∵∠AOC=∠MON=90°,∴△AOC∽△MNO,∴∠OAC=∠NMO,∵∠NMO+∠MON=90°,∴∠MON+∠OAC=90°,∴∠AGO=90°,∴OM⊥AC,∵△M′N′O′是由△MNO平移所得,∴O′M′∥OM,∴O′M′⊥AC,∵M′F=FO′,∴EM′=EO′,∵EN′∥CO,∴
,∵∠AOC=∠MON=90°,∴△AOC∽△MNO,∴∠OAC=∠NMO,∵∠NMO+∠MON=90°,∴∠MON+∠OAC=90°,∴∠AGO=90°,∴OM⊥AC,∵△M′N′O′是由△MNO平移所得,∴O′M′∥OM,∴O′M′⊥AC,∵M′F=FO′,∴EM′=EO′,∵EN′∥CO,∴![]() ,∴
,∴![]() ,∴EN′=
,∴EN′=![]() (5﹣t),在RT△EO′M′中,∵O′N′=1,EN′=
(5﹣t),在RT△EO′M′中,∵O′N′=1,EN′=![]() (5﹣t),EO′=EM′=
(5﹣t),EO′=EM′=![]() ,∴
,∴![]() ,∴t=1.
,∴t=1.
②如图2中,∵GH∥O′M′,O′M′⊥AC,∴GH⊥AC,∴∠GHE=90°,∵∠EGH+∠HEG=90°,∠AEN′+∠OAC=90°,∠HEG=∠AEN′,∴∠OAC=∠HGE,∵∠GHE=∠AOC=90°,∴△GHE∽△AOC,∴![]() ,∴EG最大时,EH最大,∵EG=GN′﹣EN′=
,∴EG最大时,EH最大,∵EG=GN′﹣EN′=![]() =
=![]() =
=![]() ,∴t=2时,EG最大值=
,∴t=2时,EG最大值=![]() ,∴EH最大值=
,∴EH最大值=![]() ,∴t=2时,EH最大值为
,∴t=2时,EH最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于点D,若AC=5,BC=12.求点D到AB的距离.

-
科目: 来源: 题型:
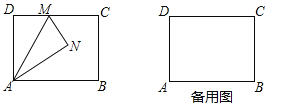
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】八边形的外角和等于 ▲ °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中,∠ABC=45°,AH⊥BC于点H,点D在AH上,且DH=CH,连结BD.
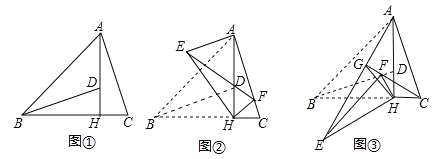
(1)求证:BD=AC;
(2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应),连接AE.
①如图②,当点F落在AC上时,(F不与C重合),若BC=4,tanC=3,求AE的长;
②如图③,当△EHF是由△BHD绕点H逆时针旋转30°得到时,设射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】角的内部到角的两边的相等的点在角的上;因此判定角平分线,需要满足两个条件:“”和“”.其一般思路是:“作垂直,证相等”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有公路l1同侧、l2异侧的两个城镇A,B,电信部门要在S区修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)
相关试题

