搜索
【题目】角的内部到角的两边的相等的点在角的上;因此判定角平分线,需要满足两个条件:“”和“”.其一般思路是:“作垂直,证相等”.
参考答案：
【答案】距离；平分线；垂直；相等
【解析】解 ：角的内部到角的两边的距离相等的点在角的平分线上;因此判定角平分线,需要满足两个条件:“垂直”和“相等”.其一般思路是:“作垂直,证相等”.
所以答案是 ：距离；平分线；垂直；相等。
【考点精析】根据题目的已知条件，利用角的平分线判定的相关知识可以得到问题的答案，需要掌握可以证明三角形内存在一个点，它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】八边形的外角和等于 ▲ °．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线与x轴交于A（6，0）、B（
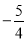，0）两点，与y轴交于点C，过抛物线上点M（1，3）作MN⊥x轴于点N，连接OM．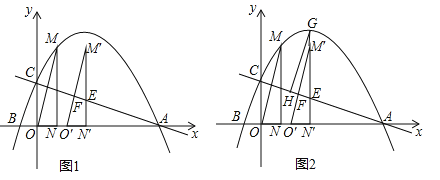
（1）求此抛物线的解析式；
（2）如图1，将△OMN沿x轴向右平移t个单位（0≤t≤5）到△O′M′N′的位置，MN′、M′O′与直线AC分别交于点E、F．
①当点F为M′O′的中点时，求t的值；
②如图2，若直线M′N′与抛物线相交于点G，过点G作GH∥M′O′交AC于点H，试确定线段EH是否存在最大值？若存在，求出它的最大值及此时t的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，△ABC中，∠ABC=45°，AH⊥BC于点H，点D在AH上，且DH=CH，连结BD．
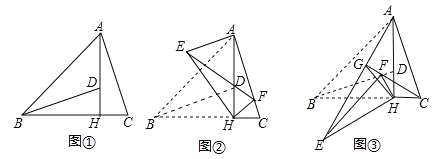
（1）求证：BD=AC；
（2）将△BHD绕点H旋转，得到△EHF（点B，D分别与点E，F对应），连接AE．
①如图②，当点F落在AC上时，（F不与C重合），若BC=4，tanC=3，求AE的长；
②如图③，当△EHF是由△BHD绕点H逆时针旋转30°得到时，设射线CF与AE相交于点G，连接GH，试探究线段GH与EF之间满足的等量关系，并说明理由．
-
科目： 来源： 题型：
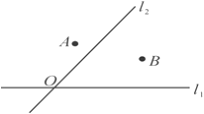
查看答案和解析>>【题目】如图，有公路l1同侧、l2异侧的两个城镇A，B，电信部门要在S区修建一座信号发射塔，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条公路l1，l2的距离也必须相等，发射塔C应修建在什么位置？请用尺规作图找出所有符合条件的点，注明点C的位置．(保留作图痕迹，不写作法)
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解参加某运动会的2 000名运动员的年龄情况,从中抽查了100名运动员的年龄,就这个问题来说,下面说法正确的是( )
A.2 000名运动员是总体
B.每个运动员是个体
C.100名运动员是抽取的一个样本
D.100名运动员的年龄是抽取的一个样本 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知点P（m﹣1，4）与点Q（2，n﹣2）关于y轴对称，则点A（m，n）所在的象限是（ ）
A.第一象限B.第二象限C.第三象限D.第四象限
相关试题
