【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于点D,若AC=5,BC=12.求点D到AB的距离.

参考答案:
【答案】![]()
【解析】试题分析:过点D作DE⊥AB于E,根据角平分线上的点到角的两边的距离相等可得CD=DE,然后利用“HL”证明△ACD和△AED全等,根据全等三角形对应边相等可得AE=AC,表示出BE,设DE=x,表示出BD,然后利用勾股定理列式计算即可得解.
试题解析:
作DE⊥AB于点E,

∵∠C=90°,AC=5,BC=12.∴AB=13
∵AD平分∠BAC,∠C=90°,DE⊥AB
∴DC=DE,
∴△AEH≌△CEB.
∴AE=AC=5,BE=13-5=8
设DE=x,则DC=x,BD=12-x,
在Rt△BDE中,∵DE2+BE2=BD2 ∴x2+82=(12-x) 2
得x=![]()
答:点D到AB的距离为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
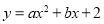 过B(﹣2,6),C(2,2)两点.
过B(﹣2,6),C(2,2)两点.(1)试求抛物线的解析式;
(2)记抛物线顶点为D,求△BCD的面积;
(3)若直线
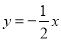 向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.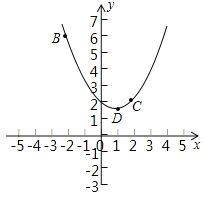
-
科目: 来源: 题型:
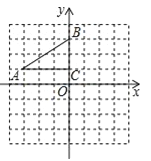
查看答案和解析>>【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD,AD∥BC,∠B=90,AD=6,AB=4,BC=9.
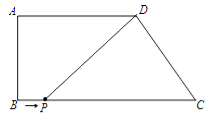
(1)求CD的长为.
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.
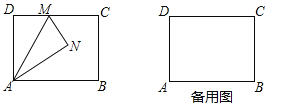
-
科目: 来源: 题型:
查看答案和解析>>【题目】八边形的外角和等于 ▲ °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线与x轴交于A(6,0)、B(
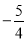 ,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.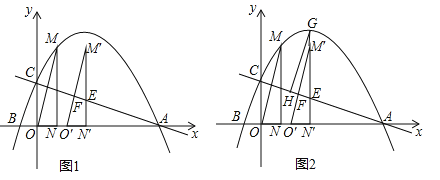
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
相关试题

