【题目】如图①,△ABC中,∠ABC=45°,AH⊥BC于点H,点D在AH上,且DH=CH,连结BD.
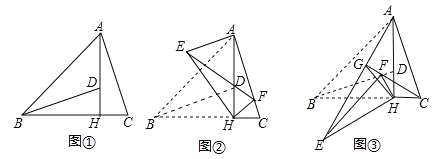
(1)求证:BD=AC;
(2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应),连接AE.
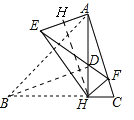
①如图②,当点F落在AC上时,(F不与C重合),若BC=4,tanC=3,求AE的长;
②如图③,当△EHF是由△BHD绕点H逆时针旋转30°得到时,设射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() =
=![]() .
.
【解析】
试题分析:(1)先判断出AH=BH,再判断出△BHD≌△AHC即可;
(2)①先根据tanC=3,求出AH=3,CH=1,然后根据△EHA≌△FHC,得到,HP=3AP,AE=2AP,最后用勾股定理即可;
②先判断出△AGQ∽△CHQ,得到![]() ,然后判断出△AQC∽△GQH,用相似比即可.
,然后判断出△AQC∽△GQH,用相似比即可.
试题解析:(1)在Rt△AHB中,∠ABC=45°,∴AH=BH,在△BHD和△AHC中,∵AH=BH,∠BHD=∠AHC,DH=CH,∴△BHD≌△AHC,∴BD=AC;
(2)①如图,在Rt△AHC中,∵tanC=3,∴![]() =3,设CH=x,∴BH=AH=3x,∵BC=4,∴3x+x=4,∴x=1,∴AH=3,CH=1,由旋转知,∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH,∴∠EHA=∠FHC,
=3,设CH=x,∴BH=AH=3x,∵BC=4,∴3x+x=4,∴x=1,∴AH=3,CH=1,由旋转知,∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH,∴∠EHA=∠FHC,![]() ,∴△EHA≌△FHC,∴∠EAH=∠C,∴tan∠EAH=tanC=3,过点H作HP⊥AE,∴HP=3AP,AE=2AP,在Rt△AHP中,
,∴△EHA≌△FHC,∴∠EAH=∠C,∴tan∠EAH=tanC=3,过点H作HP⊥AE,∴HP=3AP,AE=2AP,在Rt△AHP中,![]() ,∴
,∴![]() ,∴AP=
,∴AP=![]() ,∴AE=
,∴AE=![]() ;
;
②由①有,△AEH和△FHC都为等腰三角形,∴∠GAH=∠HCG=90°,∴△AGQ∽△CHQ,∴![]() ,∴
,∴![]() ,∵∠AQC=∠GQE,∴△AQC∽△GQH,∴
,∵∠AQC=∠GQE,∴△AQC∽△GQH,∴![]() =sin30°=
=sin30°=![]() .
.
-
科目: 来源: 题型:
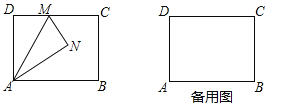
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】八边形的外角和等于 ▲ °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线与x轴交于A(6,0)、B(
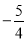 ,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.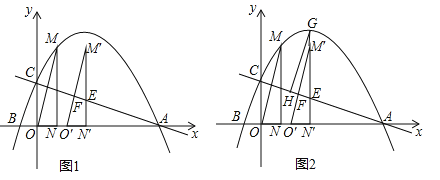
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】角的内部到角的两边的相等的点在角的上;因此判定角平分线,需要满足两个条件:“”和“”.其一般思路是:“作垂直,证相等”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有公路l1同侧、l2异侧的两个城镇A,B,电信部门要在S区修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)
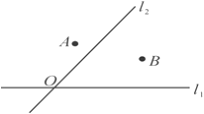
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解参加某运动会的2 000名运动员的年龄情况,从中抽查了100名运动员的年龄,就这个问题来说,下面说法正确的是( )
A.2 000名运动员是总体
B.每个运动员是个体
C.100名运动员是抽取的一个样本
D.100名运动员的年龄是抽取的一个样本
相关试题

