【题目】如图1,已知∠MON=140°,∠AOC与∠BOC互余,OC平分∠MOB,
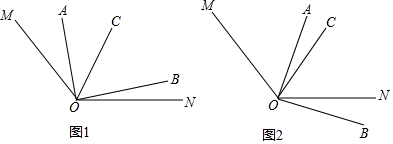
(1)在图1中,若∠AOC=40°,则∠BOC= °,∠NOB= °.
(2)在图1中,设∠AOC=α,∠NOB=β,请探究α与β之间的数量关系( 必须写出推理的主要过程,但每一步后面不必写出理由);
(3)在已知条件不变的前提下,当∠AOB绕着点O顺时针转动到如图2的位置,此时α与β之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时α与β之间的数量关系.
参考答案:
【答案】解:(1)50,40;(2)β=2α﹣40°;(3)不成立,此时此时α与β之间的数量关系为:2α+β=40°.
【解析】
(1)先根据余角的定义计算∠BOC=50°,再由角平分线的定义计算∠BOM=100°,根据角的差可得∠BON的度数;
(2)同理先计算∠MOB=2∠BOC=2(90°-α)=180°-2α,再根据∠BON=∠MON-∠BOM列等式即可;
(3)同理可得∠MOB=180°-2α,再根据∠BON+∠MON=∠BOM列等式即可.
(1)如图1,
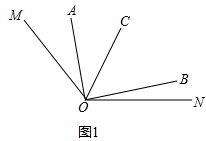
∵∠AOC与∠BOC互余,
∴∠AOC+∠BOC=90°,
∵∠AOC=40°,
∴∠BOC=50°,
∵OC平分∠MOB,
∴∠MOC=∠BOC=50°,
∴∠BOM=100°,
∵∠MON=40°,
∴∠BON=∠MON-∠BOM=140°-100°=40°,
(2)β=2α-40°,理由是:
如图1,∵∠AOC=α,
∴∠BOC=90°-α,
∵OC平分∠MOB,
∴∠MOB=2∠BOC=2(90°-α)=180°-2α,
又∵∠MON=∠BOM+∠BON,
∴140°=180°-2α+β,即β=2α-40°;
(3)不成立,此时此时α与β之间的数量关系为:2α+β=40°,
理由是:如图2,
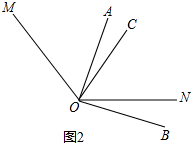
∵∠AOC=α,∠NOB=β,
∴∠BOC=90°-α,
∵OC平分∠MOB,
∴∠MOB=2∠BOC=2(90°-α)=180°-2α,
∵∠BOM=∠MON+∠BON,
∴180°-2α=140°+β,即2α+β=40°,
答:不成立,此时此时α与β之间的数量关系为:2α+β=40.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤,下面是爸爸妈妈的对话:
妈妈:“上个月萝卜的单价是
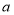 元/斤,排骨的单价比萝卜的7倍还多2元”;
元/斤,排骨的单价比萝卜的7倍还多2元”;爸爸:“今天,报纸上说与上个月相比,萝卜的单价上涨了25%,排骨的单价上涨了20%”
请根据上面的对话信息回答下列问题:
(1)请用含
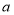 的式子填空:上个月排骨的单价是_________元/斤,这个月萝卜的单价是__________元/斤,排骨的单价是______________元/斤。
的式子填空:上个月排骨的单价是_________元/斤,这个月萝卜的单价是__________元/斤,排骨的单价是______________元/斤。(2)列式表示今天买的萝卜和排骨比上月买同重量的萝卜和排骨一共多花多少元?(结果要求化成最简)
(3)当
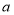 =4,求今天买的萝卜和排骨比上月买同重量的萝卜和排骨一共多花多少元?
=4,求今天买的萝卜和排骨比上月买同重量的萝卜和排骨一共多花多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】现在把一张正方形纸片按如图方式剪去一个半径为40
 厘米的圆面后得到如图纸片,且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面,则该正方形纸片的边长约为( )厘米.(不计损耗、重叠,结果精确到1厘米,
厘米的圆面后得到如图纸片,且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面,则该正方形纸片的边长约为( )厘米.(不计损耗、重叠,结果精确到1厘米, ≈1.41,
≈1.41, ≈1.73)
≈1.73)
A. 64 B. 67 C. 70 D. 73
-
科目: 来源: 题型:
查看答案和解析>>【题目】为缓解油价上涨给出租车行业带来的成本压力,某市拟调整出租车运价,调整方案见下列表格及图象(其中
 为常数)
为常数)行驶路程
收费标准
调价前
调价后
不超过
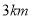 的部分
的部分起步价7元
起步价
 元
元超过
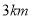 不超出
不超出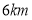 的部分
的部分每公里2元
每公里
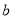 元
元超出
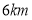 的部分
的部分每公里
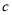 元
元设行驶路程为
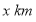 ,调价前的运价
,调价前的运价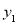 (元),调价后运价
(元),调价后运价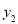 (元),如图,折线
(元),如图,折线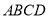 表示
表示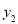 与
与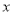 之间的函数关系式,线段
之间的函数关系式,线段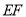 表示当
表示当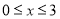 时,
时, 与
与 的函数关系式,根据图表信息,完成下列各题:
的函数关系式,根据图表信息,完成下列各题: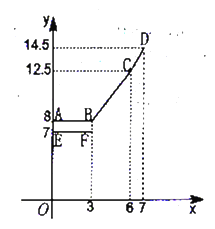
①填空:
 ,
, ,
,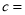 ;
;②当
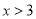 时,求
时,求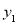 与
与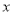 的关系,补充图中该函数的图像;
的关系,补充图中该函数的图像;③函数
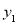 与
与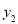 的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】七(2)班组织学生参加秋季研学活动,该班将报名参加本次活动的学生分为甲、乙、丙三组.如图,条形统计图和扇形统计图反映了学生参加研学活动的报名情况,请你根据图中的信息回答下列问题:
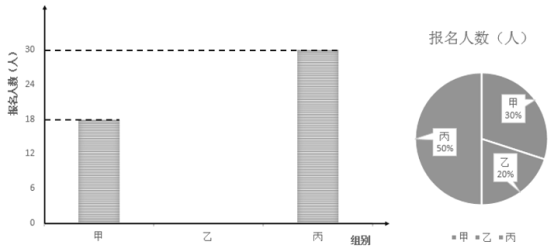
(1)七(2)班报名参加本次活动的总人数为?扇形统计图中,表示甲组部分的扇形的圆心角是多少度;
(2)补全条形统计图;
(3)研学活动中需将三组并成两组,若将乙组学生分配到甲组和丙组,乙组学生怎样分配才能使甲组学生数是丙组的三分之二?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形
 中,点
中,点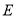 是边
是边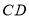 的中点,点
的中点,点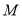 是对角线
是对角线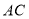 上的动点,连接
上的动点,连接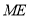 ,过点
,过点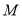 作
作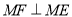 交正方形的边于点
交正方形的边于点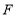 ;
;(1)当点
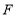 在边
在边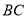 上时,①判断
上时,①判断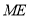 与
与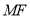 的数量关系;
的数量关系;②当
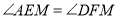 时,判断点
时,判断点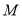 的位置;
的位置;(2)若正方形的边长为2,请直接写出点
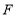 在
在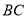 边上时,
边上时,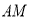 的取值范围.
的取值范围. 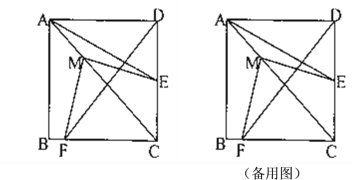
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2﹣4ac<4a2;③a>
 ;其中正确的个数为( )
;其中正确的个数为( )
A. 0 B. 1 C. 2 D. 3
相关试题

