【题目】如图,在![]() 中,D、E分别是边AC、BC上的点,若
中,D、E分别是边AC、BC上的点,若![]() ≌
≌![]() ≌
≌![]() ,
,![]() ,则
,则![]() ______ cm.
______ cm.

参考答案:
【答案】20
【解析】
根据全等三角形对应角相等,易得∠A=∠DEB=∠DEC,∠ADB=∠EDB=∠EDC;接下来根据平角的定义可得∠DEB+∠DEC=180°,∠ADB+∠EDB+∠EDC=180°,此时可得∠A=∠DEB=∠DEC=90°,∠ADB=∠EDB=∠EDC=60°,最后根据三角形内角和定理即可得到∠C的度数,进而可求出BC的长.
∵△ADB≌△EDB≌△EDC,
∴∠A=∠DEB=∠DEC,∠ADB=∠EDB=∠EDC,
∵∠DEB+∠DEC=180°,∠ADB+∠EDB+∠EDC=180°,
∴∠A=∠DEB=∠DEC=90°,∠ADB=∠EDB=∠EDC=60°.
∵在Rt△DEC中,∠DEC=90°,∠EDC=60°,
∴∠C=30°,
∴BC=2AB=2×10=20 cm.
-
科目: 来源: 题型:
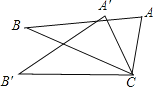
查看答案和解析>>【题目】如图,
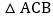 ≌
≌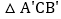 ,
,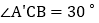 ,
,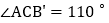 ,则
,则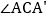 的度数是
的度数是
A.
 B.
B.  C.
C.  D.
D. 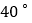
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列说法:
 形状相同的图形是全等形;
形状相同的图形是全等形; 全等形的大小相同,形状也相同;
全等形的大小相同,形状也相同; 全等三角形的面积相等;
全等三角形的面积相等; 面积相等的两个三角形全等;
面积相等的两个三角形全等; 若
若 ≌
≌ ,
, ≌
≌ ,则
,则 ≌
≌ 其中正确的说法有
其中正确的说法有
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
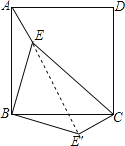
查看答案和解析>>【题目】如图,点E是正方形ABCD内的一点,点
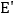 在BC边的下方,连接AE,BE,CE,
在BC边的下方,连接AE,BE,CE,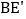 ,
,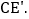 若
若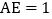 ,
,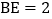 ,
,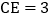 ,且
,且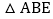 ≌
≌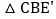 ,则
,则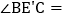 ______
______ 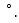
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据a、b、c的平均数为5,方差为4,那么数据a+2、b+2、c+2的平均数和方差分别为( )
A. 7,6 B. 7,4 C. 5,4 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10.动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数 ;当t=3时,OP=
(2)动点R从点B出发,以每秒8个单位长度的速度沿数轴向右匀速运动,若点P,R同时出发,问点R运动多少秒时追上点P?
(3)动点R从点B出发,以每秒8个单位长度的速度沿数轴向右匀速运动,若点P,R同时出发,问点R运动多少秒时PR相距2个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1 , x2 .
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
相关试题

