Question

【题目】如图，在矩形ABCD中，AD= AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①∠AED=∠CED；②AB=HF，③BH=HF；④BC﹣CF=2HE；⑤OE=OD；其中正确结论的序号是

Answer 1

【答案】①③⑤
【解析】解：∵在矩形ABCD中，AE平分∠BAD，∴∠BAE=∠DAE=45°，
∴△ABE是等腰直角三角形，∴AE= AB，∵AD= AB，∴AE=AD，
在△ABE和△AHD中，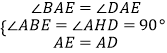

∴△ABE≌△AHD（AAS），
∴BE=DH，∴AB=BE=AH=HD，∴∠ADE=∠AED=
∴∠CED=180°-45°-67.5°=67.5°，∴∠AED=∠CED，故①正确；
∵AB=AH，∠BAE=45°，∴△ABH不是等边三角形，∴AB≠BH，∴即AB≠HF，故②错误；
∵∠EBH=90°-67.5°=22.5°，∴∠EBH=∠OHD，
在△BEH和△HDF中，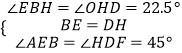

∴△BEH≌△HDF（ASA），∴BH=HF，HE=DF，故③正确；
∵HE=AE-AH=BC-CD，∴BC-CF=BC-（CD-DF）=BC-（CD-HE）=（BC-CD）+HE=HE+HE=2HE．故④正确；
∵AB=AH，∵∠AHB= ∠OHE=∠AHB（对顶角相等），
∴∠OHE=67.5°=∠AED，∴OE=OH，∵∠DHO=90°-67.5°=22.5°，∠ODH=67.5°-45°=22.5°，∴∠DHO=∠ODH，∴OH=OD，∴OE=OD=OH，故⑤正确；
综上所述，结论正确的是①③④⑤共4个．
故答案为①③④⑤.
①根据角平分线的定义可得∠BAE=∠DAE=45°，可得出△ABE是等腰直角三角形，根据等腰直角三角形的性质可得AE=AB,从而得AE=AD，然后利用“角角边”证明△ABE和△AHD全等，根据全等三角形对应边相等可得BE=DH，再根据等腰三角形两底角相等∠ADE=∠AED=67.5°，根据平角等于180°求出∠CED=67.5°，从而判断出①正确；
②判断出△ABH不是等边三角形，从而得到AB≠BH，即AB≠HF，得到②错误．
③求出∠EBH=∠OHD=22.5°，∠AEB=∠HDF=45°，然后利用“角边角”证明△BEH和△HDF全等，根据全等三角形对应边相等可得BH=HF，判断出③正确；
④根据全等三角形对应边相等可得DF=HE，然后根据HE=AE-AH=BC-CD，BC-CF==2HE．判断出④正确；
⑤求出∠AHB=67.5°，∠DHO=∠ODH=22.5°，然后根据等角对等边可得OE=OD=OH，判断出⑤正确.