Question

【题目】如图1，四边形ABCD为⊙O内接四边形，连接AC、CO、BO，点C为弧BD的中点．

（1）求证：∠DAC=∠ACO+∠ABO；

（2）如图2，点E在OC上，连接EB，延长CO交AB于点F，若∠DAB=∠OBA+∠EBA．求证：EF=EB；

（3）在（2）的条件下，如图3，若OE+EB=AB，CE=2，AB=13，求AD的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）AD=7．

【解析】试题分析：（1）如图1中，连接OA，只要证明∠CAB=∠1+∠2=∠ACO+∠ABO，由点C是 中点，推出 ，推出∠BAC=∠DAC，即可推出∠DAC=∠ACO+∠ABO；

（2）想办法证明∠EFB=∠EBF即可；

（3）如图3中，过点O作OH⊥AB，垂足为H，延长BE交HO的延长线于G，作BN⊥CF于N，作CK⊥AD于K，连接OA．作CT∠⊥AB于T．首先证明△EFB是等边三角形，再证明△ACK≌△ACT，Rt△DKC≌Rt△BTC，延长即可解决问题；

试题解析：（1）如图1中，连接OA，

∵OA=OC，∴∠1=∠ACO，

∵OA=OB，∴∠2=∠ABO，∴∠CAB=∠1+∠2=∠ACO+∠ABO，

∵点C是中点，∴，∴∠BAC=∠DAC，

∴∠DAC=∠ACO+∠ABO．

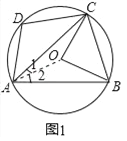
（2）如图2中，

∵∠BAD=∠BAC+∠DAC=2∠CAB，∠COB=2∠BAC，∴∠BAD=∠BOC，

∵∠DAB=∠OBA+∠EBA，∴∠BOC=∠OBA+∠EBA，

∴∠EFB=∠EBF，∴EF=EB．

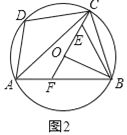
（3）如图3中，过点O作OH⊥AB，垂足为H，延长BE交HO的延长线于G，作BN⊥CF于N，作CK⊥AD于K，连接OA．作CT∠⊥AB于T．

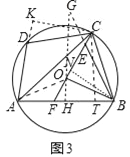
∵∠EBA+∠G=90°，∠CFB+∠HOF=90°，

∵∠EFB=∠EBF，∴∠G=∠HOF，

∵∠HOF=∠EOG，∴∠G=∠EOG，∴EG=EO，

∵OH⊥AB，∴AB=2HB，

∵OE+EB=AB，∴GE+EB=2HB，∴GB=2HB，

∴cos∠GBA= ，∴∠GBA=60°，

∴△EFB是等边三角形，设HF=a，

∵∠FOH=30°，∴OF=2FH=2a，

∵AB=13，∴EF=EB=FB=FH+BH=a+，

∴OE=EF﹣OF=FB﹣OF=﹣a，OB=OC=OE+EC=﹣a+2=﹣a，

∵NE=EF=a+，

∴ON=OE=EN=（﹣a）﹣（a+）=﹣a，

∵BO2﹣ON2=EB2﹣EN2，

∴（﹣a）2﹣（﹣a）2=（a+）2﹣（a+）2，

解得a=或﹣10（舍弃），

∴OE=5，EB=8，OB=7，

∵∠K=∠ATC=90°，∠KAC=∠TAC，AC=AC，∴△ACK≌△ACT，∴CK=CT，AK=AT，

∵，∴DC=BC，∴Rt△DKC≌Rt△BTC，∴DK=BT，

∵FT=FC=5，∴DK=TB=FB﹣FT=3，∴AK=AT=AB﹣TB=10，∴AD=AK﹣DK=10﹣3=7．