【题目】如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠BOC、∠BOF的度数.
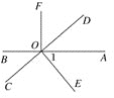
解:∵OE⊥CD( ),
∴∠DOE=_____°( ),
∵∠1=50°( ),
∴∠AOD=∠________-∠________=________°,
∵∠BOC与∠AOD为_______角(____________),
∴∠BOC=∠________=∠_________°(_____________),
∵OD平分∠AOF(______________),
且∠AOD=____________°(______________),
∴∠AOF=2∠__________=________°( ),
∵∠BOF+∠AOF=______°( ),
∴∠BOF=______°-∠AOF=_________°.
参考答案:
【答案】已知,90,垂直的定义,已知,DOE,1,40,对顶,已知,AOD,40,对顶角相等,已知,40,已求,AOD,80,角平分线定义,180,邻补角定义,180,100.
【解析】
根据垂直的定义,可得∠DOE,根据对顶角的定义,可得∠BOC,根据角平分线的定义,可得∠AOF,根据邻补角的定义,可得答案.
解:∵OE⊥CD( 已知),
∴∠DOE=90°( 垂直的定义),
∵∠1=50°( 已知),
∴∠AOD=∠DOE-∠1=40°,
∵∠BOC与∠AOD为对顶角( 对顶角的定义),
∴∠BOC=∠AOD=40°( 对顶角相等),
∵OD平分∠AOF( 已知),
且∠AOD=40°( 已求),
∴∠AOF=2∠AOD=80°( 角平分线的定义),
∵∠BOF+∠AOF=180°( 邻补角的定义),
∴∠BOF=180°-∠AOF=100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 的长;
的长;
(Ⅱ)若 =
=  ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
销售价格x
20
25
30
50
销售量y
15
12
10
6
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式;
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断

A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC. (Ⅰ)求证:直线DM是⊙O的切线;
(Ⅱ)求证:DE2=DFDA.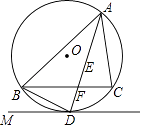
-
科目: 来源: 题型:
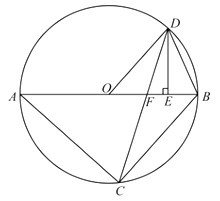
查看答案和解析>>【题目】如图,已知
 内接于
内接于  ,
,  是直径,点
是直径,点  在
在 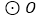 上,
上, 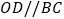 ,过点
,过点  作
作  ,垂足为
,垂足为  ,连接
,连接 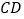 交
交 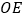 边于点
边于点 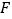 .
.
(1)求证: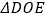 ∽
∽ 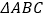 ;
;
(2)求证: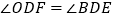 ;
;
(3)连接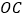 ,设
,设 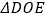 的面积为
的面积为 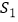 ,四边形
,四边形 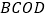 的面积为
的面积为 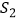 ,若
,若 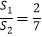 ,求
,求 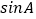 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A.
 B.
B.  C. 3 D.
C. 3 D. 
相关试题

