【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数y=![]() (k>0)图象与AC边交于点E.
(k>0)图象与AC边交于点E.

(1)请用k的表示点E,F的坐标;
(2)若△OEF的面积为9,求反比例函数的解析式.
参考答案:
【答案】(1)E( ![]() ,4),F(6,
,4),F(6,![]() );(2)y=
);(2)y=![]()
【解析】
试题分析:(1)易得E点的纵坐标为4,F点的横坐标为6,把它们分别代入反比例函数y=![]() (k>0)即可得到E点和F点的坐标;
(k>0)即可得到E点和F点的坐标;
(2)分别用矩形面积和能用图中的点表示出的三角形的面积表示出所求的面积,解方程即可求得k的值.
解:(1)E( ![]() ,4),F(6,
,4),F(6,![]() );
);
(2)∵E,F两点坐标分别为E( ![]() ,4),F(6,
,4),F(6,![]() ),
),
∴S△ECF=![]() E×CF=
E×CF=![]() (6﹣
(6﹣![]() k)(4﹣
k)(4﹣![]() k),
k),
∴S△EOF=S矩形AOBC﹣S△AOE﹣S△BOF﹣S△ECF
=24﹣![]() k﹣
k﹣![]() k﹣S△ECF
k﹣S△ECF
=24﹣k﹣![]() (6﹣
(6﹣![]() k)(4﹣
k)(4﹣![]() k),
k),
∵△OEF的面积为9,
∴24﹣k﹣![]() (6﹣
(6﹣![]() k)(4﹣
k)(4﹣![]() k)=9,
k)=9,
整理得,![]() =6,
=6,
解得k=12.
∴反比例函数的解析式为y=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知D是△ABC的边BC所在直线上的一点,与B,C不重合,过D分别作DF∥AC交AB所在直接于F,DE∥AB交AC所在直线于E.若∠A=80°,则∠FDE的度数是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣mx2+4x+2m与x轴交于点A(α,0),B(β,0),且
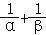 =﹣2,
=﹣2,
(1)求抛物线的解析式.
(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l的对称点为E,是否存在x轴上的点M,y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列填空.如右图,已知AD⊥BC,EF⊥BC,∠1=∠2. 求证: DG∥BA.

证明:∵AD⊥BC,EF⊥BC(已知)
∴∠EFB=∠ADB=90° ( )
∴ ∥ ( )
∴∠1=∠BAD ( )
又∵∠1=∠2 (已知)
∴ (等量代换)
∴DG∥BA. ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.

(1)求证:AB=BE;
(2)若PA=2,cosB=
 ,求⊙O半径的长.
,求⊙O半径的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=
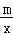 的图象的两个交点.
的图象的两个交点.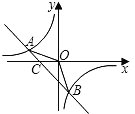
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求方程kx+b﹣
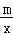 =0的解(请直接写出答案);
=0的解(请直接写出答案);(4)求不等式kx+b﹣
 <0的解集(请直接写出答案).
<0的解集(请直接写出答案).
相关试题

