【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△AHD;②HE=CE;③H是BF的中点;④AB=HF;其中正确命题的个数为__________个.
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△AHD;②HE=CE;③H是BF的中点;④AB=HF;其中正确命题的个数为__________个.
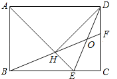
参考答案:
【答案】3
【解析】
根据题意,可知,ABE与AHD是等腰直角三角形,进而可得,AH=AB,AD=AE,根据三角形全等的判定方法,可证△ABE≌△AHD,①正确;根据矩形,等腰直角三角形和全等三角形的性质,可知,DH=AH=AB=BE,AD=AE=BC,进而,可得HE=CE,②正确;
根据等腰三角形的性质和三角形内角和定理,可得∠EBH=∠OHD=22.5°,进而可证明BEHHDF,即即H是BF的中点,③正确;由AB=AH,∠BAE=45°,可知,ABH不是等边三角形,进而可知,④错误.
∵在矩形ABCD中,∠BAD的平分线交BC于点E,DH⊥AE于点H,
∴∠BAE=∠HAD=45°,∠ABE=∠AHD=90°,
∴ABE与AHD是等腰直角三角形,
∴AD=![]() AH,AE=
AH,AE=![]() AB,
AB,
∵AD=![]() AB,
AB,
∴AH=AB,AD=AE,
在ABE与AHD中,
∵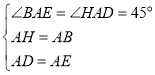
∴△ABE≌△AHD(SAS),故①正确;
∵在矩形ABCD中,ABE与AHD是等腰直角三角形,△ABE≌△AHD,
∴DH=AH=AB=BE,AD=AE=BC
∴AE-AH=BC-BE ,
∴HE=CE,故②正确;
∵AB=AH,
∴![]() ,
,
∴∠OHE=∠AHB=67.5°,
∴∠DHO=90°-67.5°=22.5°,
∵∠EBH=90°-67.5°=22.5°,
∴∠EBH=∠OHD,
在BEH和HDF中
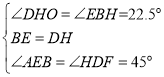
∴BEHHDF(ASA),
∴BH=HF,
即H是BF的中点,故③正确;
∵AB=AH,∠BAE=45°,
∴ABH不是等边三角形,
∴AB≠BH,
∴AB≠HF,故④错误,
综上所述,正确命题有3个,
故答案是:3
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与另一腰的夹角为360,则该等腰三角形的底角的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 的垂直平分线
的垂直平分线 交
交 于点
于点 ,交
,交 于点
于点 ,且
,且 ,添加一个条件,能证明四边形
,添加一个条件,能证明四边形 为正方形的是________.
为正方形的是________.①
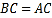 ; ②
; ② ; ③
; ③ ; ④
; ④ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,O为坐标原点,点A的坐标是(2,2),若点P在x轴上,且△APO是直角三角形,则点P的坐标是 ________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a+2)
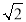 ﹣b+3=0,其中a、b为有理数,那么a= ,b= ;
﹣b+3=0,其中a、b为有理数,那么a= ,b= ;(2)如果2b﹣a﹣(a+b﹣4)
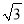 =5,其中a、b为有理数,求3a+2b的平方根.
=5,其中a、b为有理数,求3a+2b的平方根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
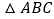 ,按如下步骤作图:
,按如下步骤作图:①分别以
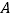 、
、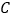 为圆心,以大于
为圆心,以大于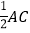 的长为半径在
的长为半径在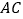 两边作弧,交于两点
两边作弧,交于两点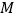 、
、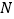 ;
;②作直线
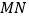 ,分别交
,分别交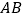 、
、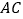 于点
于点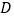 、
、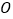 ;
;③过
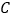 作
作 交
交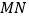 于点
于点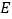 ,连接
,连接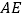 、
、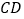 .
.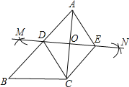
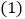 求证:四边形
求证:四边形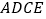 是菱形;
是菱形;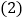 当
当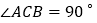 ,
,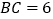 ,
,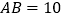 ,求四边形
,求四边形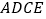 的面积.
的面积. -
科目: 来源: 题型:
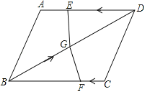
查看答案和解析>>【题目】如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.
(1)试证明:AD∥BC.
(2)在移动过程中,小芹发现当点G的运动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的运动速度取哪些值时,△DEG与△BFG全等.
相关试题

