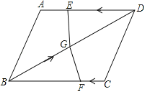
【题目】如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.
(1)试证明:AD∥BC.
(2)在移动过程中,小芹发现当点G的运动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的运动速度取哪些值时,△DEG与△BFG全等.
参考答案:
【答案】(1)见解析;(2)点G的速度为1.5或3或1.
【解析】
(1)根据三角形全等的判定和性质定理,得到△ABD≌△CDB,进而,可证明AD∥BC;
(2)设运动时间为t,点G的运动速度为v,根据全等三角形的性质,分四种情况进行讨论:①当0<t≤![]() 时,若△DEG≌△BFG,若△DEG≌△BGF;②当
时,若△DEG≌△BFG,若△DEG≌△BGF;②当![]() <t≤
<t≤![]() 时,若△DEG≌△BFG,若△DEG≌△BGF.
时,若△DEG≌△BFG,若△DEG≌△BGF.
(1)证明:在△ABD和△CDB中
,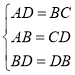
∴△ABD≌△CDB,
∴∠ADB=∠CBD,
∴AD∥BC;
(2)解:设运动时间为t,点G的运动速度为v,
当0<t≤![]() 时,若△DEG≌△BFG,则
时,若△DEG≌△BFG,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴v=3;
若△DEG≌△BGF,则![]() ,
,
∴![]() ,
,
∴![]() (舍去);
(舍去);
当![]() <t≤
<t≤![]() 时,若△DEG≌△BFG,则
时,若△DEG≌△BFG,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴v=1.5;
若△DEG≌△BGF,则![]() ,
,
∴![]() ,
,
∴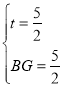 ,
,
∴v=1.
综上,点G的速度为1.5或3或1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=
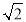 AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△AHD;②HE=CE;③H是BF的中点;④AB=HF;其中正确命题的个数为__________个.
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△AHD;②HE=CE;③H是BF的中点;④AB=HF;其中正确命题的个数为__________个.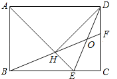
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a+2)
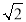 ﹣b+3=0,其中a、b为有理数,那么a= ,b= ;
﹣b+3=0,其中a、b为有理数,那么a= ,b= ;(2)如果2b﹣a﹣(a+b﹣4)
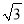 =5,其中a、b为有理数,求3a+2b的平方根.
=5,其中a、b为有理数,求3a+2b的平方根. -
科目: 来源: 题型:
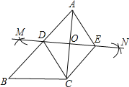
查看答案和解析>>【题目】如图,已知
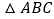 ,按如下步骤作图:
,按如下步骤作图:①分别以
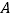 、
、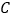 为圆心,以大于
为圆心,以大于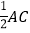 的长为半径在
的长为半径在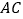 两边作弧,交于两点
两边作弧,交于两点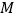 、
、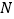 ;
;②作直线
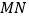 ,分别交
,分别交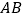 、
、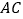 于点
于点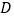 、
、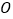 ;
;③过
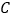 作
作 交
交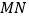 于点
于点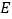 ,连接
,连接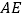 、
、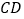 .
.
 求证:四边形
求证:四边形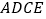 是菱形;
是菱形; 当
当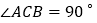 ,
,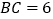 ,
,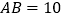 ,求四边形
,求四边形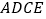 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读)
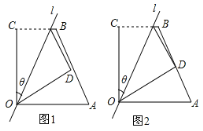
如图1,四边形OABC中,OA=a,OC=8,BC=6,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(理解)
若点D与点A重合,则这个操作过程为FZ[45°,8];
(尝试)
(1)若点D与OA的中点重合,则这个操作过程为FZ[____,____];
(2)若点D恰为AB的中点(如图2),求θ的值;
(应用)
经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上,直线l与AB相交于点F,试画出图形并解决下列问题:
①求出a的值;
②若P为边OA上一动点,连接PE、PF,请直接写出PE+PF的最小值.
(备注:等腰直角三角形的三边关系满足
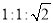 或
或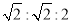 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店销售一批衬衫,每件进价
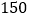 元,开始以每件
元,开始以每件 元的价格销售,每星期能卖出
元的价格销售,每星期能卖出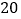 件,后来因库存积压,决定降价销售,经两次降价后的每件售价
件,后来因库存积压,决定降价销售,经两次降价后的每件售价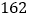 元,每星期能卖出
元,每星期能卖出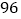 件.
件.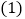 已知两次降价百分率相同,求每次降价的百分率;
已知两次降价百分率相同,求每次降价的百分率; 聪明的店主在降价过程中发现,适当的降价既可增加销售又可增加收入,且每件衬衫售价每降低
聪明的店主在降价过程中发现,适当的降价既可增加销售又可增加收入,且每件衬衫售价每降低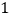 元,销售会增加
元,销售会增加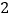 件,若店主想要每星期获利
件,若店主想要每星期获利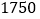 元,应把售价定为多少元?
元,应把售价定为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
相关试题

