【题目】在四边形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3![]() .分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
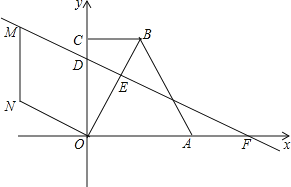
(1)求点B的坐标;
(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;
(3)点M在(2)中直线DE上,四边形ODMN是菱形,求N的坐标.
参考答案:
【答案】(1)点B的坐标为(3,6);(2)y=﹣![]() x+5;(3)N的坐标为(﹣2
x+5;(3)N的坐标为(﹣2![]() ,
,![]() ).
).
【解析】
试题分析:(1)作BH⊥OA于H,根据矩形的性质求出OH的长,根据勾股定理求出BH的长,得到点B的坐标;
(2)作EG⊥OA于G,得到△OGE∽△OHB,根据题意和相似三角形的性质求出点E、D的坐标,运用待定系数法求出直线DE的解析式;
(3)作MP⊥y轴于点P,得到△MPD∽△FOD,根据相似三角形的性质和勾股定理计算即可.
解:如图1,作BH⊥OA于H,则四边形OHBC为矩形,
∴OH=CB=3,
∴AH=OA﹣OH=3,
∴BH=![]() =6,
=6,
∴点B的坐标为(3,6);
(2)如图1,作EG⊥OA于G,则EG∥BH,

∴△OGE∽△OHB,
∴![]() =
=![]() =
=![]() ,
,
∵OE=2EB,
∴![]() =
=![]() ,又OH=3,BH=6,
,又OH=3,BH=6,
∴OG=2,EG=4,
∴点E的坐标为(2,4),
∵OC=BH=6,OD=5,
∴点D的坐标为(0,5),
设直线DE的解析式为y=kx+b,
∴![]() ,
,
解得,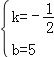 ,
,
∴直线DE的解析式为y=﹣![]() x+5;
x+5;
(3)如图2,作MP⊥y轴于点P,
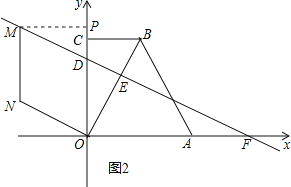
∵四边形ODMN是菱形,
∴DM=MN=NO=OD=5,
∵MP∥OA,
∴△MPD∽△FOD,
∴![]() =
=![]() =
=![]() ,
,
当y=0,即﹣![]() x+5=0时,x=10,
x+5=0时,x=10,
∴点F的坐标为(0,10),
∴DF=![]() =5
=5![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
解得,MP=2![]() ,PD=
,PD=![]() ,
,
∴OP=5+![]() ,
,
∴N的坐标为(﹣2![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中与多项式2x-(-3y-4z)相等的是( )
A、2x+(-3y+4z) B、2x+(3y-4z)
C、2x+(-3y-4z) D、2x+(3y+4z)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某经销商用8000元购进了一种衬衫,他以每件58元的价格出售,很快售完,又用17600元购进同种衬衫,数量是第一次的2倍,但每件进价比第一次多4元,服装店仍按每件58元出售,全部售完.
(1)设他第一次购进这种衬衫的价格为x元/件,则他第一次购进这种衬衫 件,他第二次购进这种衬衫 件;
(2)问他在这次服装生意中共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标为:A(2,4),B(4,3),C(1,1),直线l过点(﹣1,0)且平行于y轴.
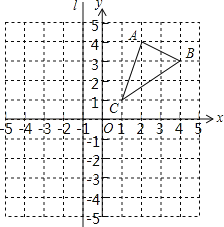
(1)在图中作出△ABC关于x轴对称的△A′B′C′;
(2)作出△ABC关于直线l对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣6x+k=0.
(1)当它有两个实数根时,求k的范围;
(2)当k=﹣11时,假设方程两根是x1,x2,求x12+x22+8的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简,求值
(1)5x2y+{xy﹣[5x2y﹣(7xy2+
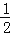 xy)]﹣(4x2y+xy)}﹣7xy2,其中x=﹣
xy)]﹣(4x2y+xy)}﹣7xy2,其中x=﹣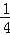 ,y=﹣16.
,y=﹣16.(2)A=4x2﹣2xy+4y2,B=3x2﹣6xy+3y2,且|x|=3,y2=16,|x+y|=1,求4A+[(2A﹣B)﹣3(A+B)]的值.
(3)如果m﹣3n+4=0,求:(m﹣3n)2+7m3﹣3(2m3n﹣m2n﹣1)+3(m3+2m3n﹣m2n+n)﹣m﹣10m3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )

A.
 B.
B. C.1 D.
C.1 D.
相关试题

