【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?

参考答案:
【答案】(1)y=-2x+60(10≤x≤18);(2)销售价为18元时,每天的销售利润最大,最大利润是192元.(3)15元.
【解析】
试题(1)设函数关系式y=kx+b,把(10,40),(18,24)代入求出k和b即可,由成本价为10元/千克,销售价不高于18元/千克,得出自变量x的取值范围;
(2)根据销售利润=销售量×每一件的销售利润得到w和x的关系,利用二次函数的性质得最值即可;
(3)先把y=150代入(2)的函数关系式中,解一元二次方程求出x,再根据x的取值范围即可确定x的值.
试题解析:(1)设y与x之间的函数关系式y=kx+b,把(10,40),(18,24)代入得
![]() ,
,
解得![]() ,
,
∴y与x之间的函数关系式y=-2x+60(10≤x≤18);
(2)W=(x-10)(-2x+60)
=-2x2+80x-600,
对称轴x=20,在对称轴的左侧y随着x的增大而增大,
∵10≤x≤18,
∴当x=18时,W最大,最大为192.
即当销售价为18元时,每天的销售利润最大,最大利润是192元.
(3)由150=-2x2+80x-600,
解得x1=15,x2=25(不合题意,舍去)
答:该经销商想要每天获得150元的销售利润,销售价应定为15元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为
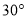 ,底部B点的俯角为
,底部B点的俯角为 ,小华在五楼找到一点D,利用三角板测得A点的俯角为
,小华在五楼找到一点D,利用三角板测得A点的俯角为 (如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠BCA=90°,BC=AC,直角顶点C在y轴上,锐角顶点A在x轴上.
(1)如图①,若点C的坐标是(0,-1),点A的坐标是(-3,0),求B点的坐标;
(2)如图②,若x轴恰好平分∠BAC,BC与x轴交于点D,过点B作BE⊥x轴于E,问AD与BE有怎样的数量关系,并说明理由;
(3)如图③,直角边AC在两坐标轴上滑动,使点B在第四象限内,过B点作BF⊥x轴于F,在滑动的过程中,猜想OC、BF、OA之间的关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别
时间
 小时
小时
频数
 人数
人数
频率
A
6

B

a

C

10

D

8
b
E

4

合计
1
请根据图表中的信息,解答下列问题:
 表中的
表中的 ______,
______, ______,中位数落在______组,将频数分布直方图补全;
______,中位数落在______组,将频数分布直方图补全; 估计该校2000名学生中,每周课余阅读时间不足
估计该校2000名学生中,每周课余阅读时间不足 小时的学生大约有多少名?
小时的学生大约有多少名? 组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.
组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”,
(1)如图△ABC中,AB=AC=
 ,BC=2,求证:△ABC是“美丽三角形”;
,BC=2,求证:△ABC是“美丽三角形”;(2)在Rt△ABC中,∠C=90°,AC=2
 ,若△ABC是“美丽三角形”,求BC的长.
,若△ABC是“美丽三角形”,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)证明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的长,

-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡镇风力资源丰富,为了实现低碳环保,该乡镇决定开展风力发电,打算购买10台风力发电机组.现有A,B两种型号机组,其中A型机组价格为12万元/台,月均发电量为2.4万kw.h;B型机组价格为10万元/台,月均发电量为2万kw.h.经预算该乡镇用于购买风力发电机组的资金不高于105万元.
(1)请你为该乡镇设计几种购买方案;
(2)如果该乡镇用电量不低于20.4万kw.h/月,为了节省资金,应选择那种购买方案?
相关试题

