【题目】如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)证明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的长,

参考答案:
【答案】(1)见解析;(2)EC=4.
【解析】
(1)由AB=AC,可知∠B=∠C,再由DE⊥BC,可知∠F+∠C=90°,∠BDE+∠B=90,然后余角的性质可推出∠F=∠BDE,再根据对顶角相等进行等量代换即可推出∠F=∠FDA,于是得到结论;
(2)根据解直角三角形和等边三角形的性质即可得到结论.
(1)∵AB=AC,
∴∠B=∠C,
∵FE⊥BC,
∴∠F+∠C=90°,∠BDE+∠B=90°,
∴∠F=∠BDE,
而∠BDE=∠FDA,
∴∠F=∠FDA,
∴AF=AD,
∴△ADF是等腰三角形;
(2)∵DE⊥BC,
∴∠DEB=90°,
∵∠B=60°,BD=4,
∴BE=![]() BD=2,
BD=2,
∵AB=AC,
∴△ABC是等边三角形,
∴BC=AB=AD+BD=6,
∴EC=BC﹣BE=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别
时间
 小时
小时
频数
 人数
人数
频率
A
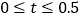
6

B

a

C

10

D

8
b
E

4

合计
1
请根据图表中的信息,解答下列问题:
 表中的
表中的 ______,
______, ______,中位数落在______组,将频数分布直方图补全;
______,中位数落在______组,将频数分布直方图补全; 估计该校2000名学生中,每周课余阅读时间不足
估计该校2000名学生中,每周课余阅读时间不足 小时的学生大约有多少名?
小时的学生大约有多少名? 组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.
组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”,
(1)如图△ABC中,AB=AC=
 ,BC=2,求证:△ABC是“美丽三角形”;
,BC=2,求证:△ABC是“美丽三角形”;(2)在Rt△ABC中,∠C=90°,AC=2
 ,若△ABC是“美丽三角形”,求BC的长.
,若△ABC是“美丽三角形”,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡镇风力资源丰富,为了实现低碳环保,该乡镇决定开展风力发电,打算购买10台风力发电机组.现有A,B两种型号机组,其中A型机组价格为12万元/台,月均发电量为2.4万kw.h;B型机组价格为10万元/台,月均发电量为2万kw.h.经预算该乡镇用于购买风力发电机组的资金不高于105万元.
(1)请你为该乡镇设计几种购买方案;
(2)如果该乡镇用电量不低于20.4万kw.h/月,为了节省资金,应选择那种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在等腰
,在等腰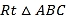 中,
中, ,点E在AC上
,点E在AC上 且不与点A、C重合
且不与点A、C重合 ,在
,在 的外部作等腰
的外部作等腰 ,使
,使 ,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF. 请直接写出线段AF,AE的数量关系;
请直接写出线段AF,AE的数量关系; 将
将 绕点C逆时针旋转,当点E在线段BC上时,如图
绕点C逆时针旋转,当点E在线段BC上时,如图 ,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
,连接AE,请判断线段AF,AE的数量关系,并证明你的结论; 若
若 ,
, ,在图
,在图 的基础上将
的基础上将 绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.


-
科目: 来源: 题型:
查看答案和解析>>【题目】课本“目标与评定”中有这样一道思考题:如图钢架中∠A=20°,焊上等边的钢条P1P2,P2P3,P3P4,P4P5…来加固钢架,若P1A=P1P2,问这样的钢条至多需要多少根?
(1)请将下列解答过程补充完整:
答案:∵∠A=20°,P1A=P1P2,∴∠P1P2A= .
又P1P2=P2P3=P3P4=P4P5,∴∠P2P1P3=P2P3P1=40°,
同理可得,∠P3P2P4=P3P4P2=60°,∠P4P3P5=P4P5P3= ,
∴∠BP4P5=∠CP5P4=100°>90°,
∴对于射线P4B上任意一点P6(点P4除外),P4P5<P5P6,
∴这样的钢架至多需要 根.
(2)继续探究:当∠A=15°时,这样的钢条至多需要多少根?
(3)当这样的钢条至多需要8根时,探究∠A的取值范围.

相关试题

