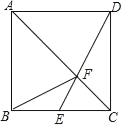
【题目】如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①△ABF≌△ADF;②S△ADF=2S△CEF;③tan∠EBF=![]() ;④S△ABF=4S△BEF,其中正确结论的个数是( )
;④S△ABF=4S△BEF,其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】分析:根据SAS可以推出△AFD≌△AFB,故①正确;即可推出S△ABF=S△ADF,由BE=EC=![]() BC=
BC=![]() AD,AD∥EC,推出
AD,AD∥EC,推出![]() =
=![]() ,可得S△ABF=S△ADF=4S△CEF,S△CEF=S△BEF,故②错误,④正确,求出CM=
,可得S△ABF=S△ADF=4S△CEF,S△CEF=S△BEF,故②错误,④正确,求出CM=![]() BC,即可判断③.
BC,即可判断③.
详解:∵四边形ABCD是正方形,
∴AD∥CB,AD=BC=AB,∠FAD=∠FAB,
在△AFD和△AFB中,
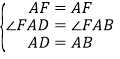 ,
,
∴△AFD≌△AFB,故①正确,
∴S△ABF=S△ADF,
∵BE=EC=![]() BC=
BC=![]() AD,AD∥EC,
AD,AD∥EC,
∴![]() =
=![]() ,
,
∴S△ADF=4S△CEF,S△CFE=4S△BEF,
故②错误;④正确;
延长BF交CD于M,
∵四边形ABCD是正方形,
∴AB∥CD,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴CM=![]() AB=
AB=![]() CD=
CD=![]() BC,
BC,
∴tan∠EBF=![]() =
=![]() ,故③正确;
,故③正确;
即正确的个数是3,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2010年开始合肥市开展了“体育、艺术2+1”活动,我校根据实际情况,决定主要开设A:乒乓球,B:象棋,C:篮球,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图甲、乙所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题:
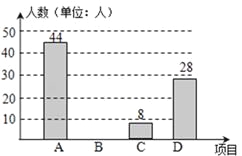

(1)样本中喜欢B项目的人数百分比是 ,其所在扇形统计图中的圆心角的度数是 ;
(2)把条形统计图补充完整;
(3)已知我校有学生2400人,根据样本估计全校喜欢乒乓球的人数是多少?
-
科目: 来源: 题型:
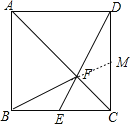
查看答案和解析>>【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B、C重合),CN⊥DM,CN与AB交于点N,连接OM、ON、MN.下列四个结论:①△CNB≌△DMC;②△CON≌△DOM;③AN2+CM2=MN2;④若AB=2,则S△OMN的最小值是
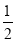 .其中正确结论的个数是( )
.其中正确结论的个数是( )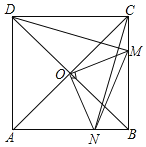
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
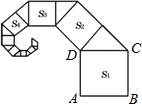
A. (
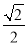 )2013B. (
)2013B. (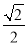 )2014C. (
)2014C. (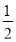 )2013D. (
)2013D. (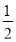 )2014
)2014 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将平行四边形ABCD折叠,使顶点D恰好落在AB边上的点M处,折痕为AN,有以下四个结论①MN∥BC;②MN=AM;③四边形MNCB是矩形;④四边形MADN是菱形,以上结论中,你认为正确的有_____________(填序号).
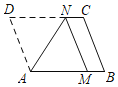
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个盛水的圆柱体玻璃容器,它的底面半径为
 (容器厚度忽略不计),容器内水的高度为
(容器厚度忽略不计),容器内水的高度为 .
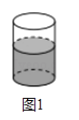
.(1)如图1, 容器内水的体积为_
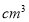 (结果保留
(结果保留 ).
).
(2)如图2,把一根半径为
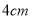 ,高为
,高为 的实心玻璃棒插入水中(玻璃棒完全淹没于水中),求水面上升的高度是多少?
的实心玻璃棒插入水中(玻璃棒完全淹没于水中),求水面上升的高度是多少?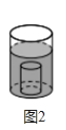
(3)如图3,若把一根半径为
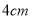 ,足够长的实心玻璃棒插入水中,求水面上升的高度是多少?
,足够长的实心玻璃棒插入水中,求水面上升的高度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,每个小正方形的边长为1cm
(1)求四边形ABCD的面积;
(2)四边形ABCD中有直角吗?若有,请说明理由.

相关试题

