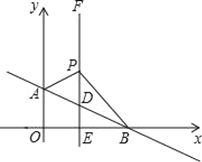
【题目】如图,平面直角坐标系中,直线AB:y=﹣![]() x+b交y轴于A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
x+b交y轴于A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
(1)直线AB的表达式为__________________;
(2)①求△ABP的面积(用含n的代数式表示);
②当S△ABP=2时,求点P的坐标;
③在②的条件下,以PB为边在第一象限作等腰直角三角形BPC,请直接写出点C的坐标.
参考答案:
【答案】(1)y=﹣![]() x+1;(2)①S△ABP=
x+1;(2)①S△ABP=![]() ;②P(1,2);③(3,4)或(5,2)或(3,2).
;②P(1,2);③(3,4)或(5,2)或(3,2).
【解析】
(1)把A的坐标代入直线AB的解析式即可求得b的值,由此即可求得直线AB的解析式;(2)①过点A作AM⊥PD,垂足为M,求得AM的长,再求得△BPD和△PAB的面积,二者的和即为△ABP的面积;②当S△ABP=2时,代入①中所得的代数式,求得n值,即可求得点P的坐标;③分P是直角顶点且BP=PC、B是直角顶点且BP=BC 、C是直角顶点且CP=CB三种情况求点C的坐标即可.
(1)∵y=-![]() x+b经过A(0,1),
x+b经过A(0,1),
∴b=1,
∴直线AB的解析式是y=-![]() x+1;
x+1;
故答案为:y=-![]() x+1;
x+1;
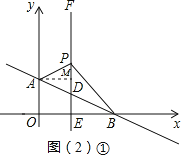
(2)①过点A作AM⊥PD,垂足为M,则有AM=1,
∵x=1时,y=-![]() x+1=
x+1=![]() ,P在点D的上方,
,P在点D的上方,
∴PD=n-![]() ,S△APD=
,S△APD=![]() PDAM=
PDAM=![]() ×1×(n
×1×(n![]() )=
)=![]() n
n![]() ,
,
由点B(3,0),可知点B到直线x=1的距离为2,即△BDP的边PD上的高长为2,
∴S△BPD=![]() PD×2=n-
PD×2=n-![]() ,
,
∴S△PAB=S△APD+S△BPD=![]() n-
n-![]() +n-
+n-![]() =
=![]() n-1;
n-1;
②当S△ABP=2时,![]() n-1=2,
n-1=2,
解得n=2,
∴点P(1,2).
③∵E(1,0),
∴PE=BE=2,
∴∠EPB=∠EBP=45°.
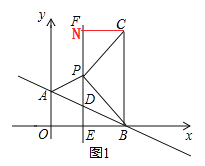
第1种情况,如图1,∠CPB=90°,BP=PC,
过点C作CN⊥直线x=1于点N.
∵∠CPB=90°,∠EPB=45°,
∴∠NPC=∠EPB=45°,
在△CNP与△BEP中,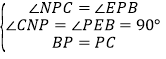 ,
,
∴△CNP≌△BEP,
∴PN=NC=EB=PE=2,
∴NE=NP+PE=2+2=4,
∴C(3,4).
第2种情况,如图2,∠PBC=90°,BP=BC,
过点C作CF⊥x轴于点F.
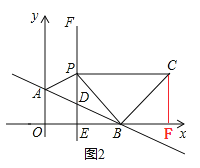
∵∠PBC=90°,∠EBP=45°,
∴∠CBF=∠PBE=45°,
在△CBP与△PBE中,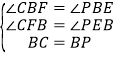 ,
,
∴△CBF≌△PBE.
∴BF=CF=PE=EB=2,
∴OF=OB+BF=3+2=5,
∴C(5,2).
第3种情况,如图3,∠PCB=90°,CP=CB,
∴∠CPB=∠CBP=45°,
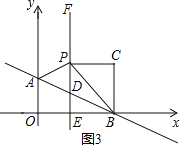
∵∠EPB=∠EBP=45°,
∴∠PCB=∠CBE=∠EPC=90°,
∴四边形EBCP为矩形,
∵CP=CB,
∴四边形EBCP为正方形,
∴PC=CB=PE=EB=2,
∴C(3,2).
∴以PB为边在第一象限作等腰直角三角形BPC,点C的坐标是(3,4)或(5,2)或(3,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数的图像与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)一次函数的函数关系式;
(2)若直线AB上有一点C,且△BOC的面积为2,求点C 的坐标;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,数轴上从左到右的三个点A,B,C所对应数的分别为a,b,c.其中点A、点B两点间的距离AB的长是2019,点B、点C两点间的距离BC的长是1000,

(1)若以点C为原点,直接写出点A,B所对应的数;
(2)若原点O在A,B两点之间,求|a|+|b|+|b﹣c|的值;
(3)若O是原点,且OB=19,求a+b﹣c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠B=90°,AB∥DF,AB=3cm,BD=8cm,点C是线段BD上一动点,点E是直线DF上一动点,且始终保持AC⊥CE.
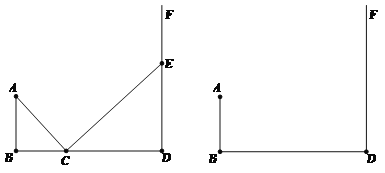
(1)试说明:∠ACB =∠CED
(2)若AC=CE ,试求DE的长
(3)在线段BD的延长线上,是否存在点C,使得AC=CE,若存在,请求出DE的长及△AEC的面积;若不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3a(a>0)与x轴交于A、B两点(点A在点B左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
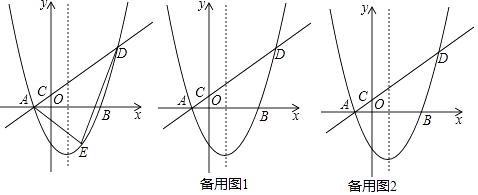
(1)直接写出点A的坐标,并用含a的式子表示直线l的函数表达式(其中k、b用含a的式子表示).
(2)点E为直线l下方抛物线上一点,当△ADE的面积的最大值为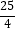 时,求抛物线的函数表达式;
时,求抛物线的函数表达式;
(3)设点P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…,根据这个规律,第2 018个点的坐标为( )
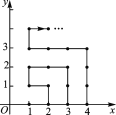
A. (45,9) B. (45,11) C. (45,7) D. (46,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若10m=5,10n=3,则102m+3n= .
【答案】675.
【解析】102m+3n=102m103n=(10m)2(10n)3=5233=675,
故答案为:675.
点睛:此题考查了幂的乘方与积的乘方, 同底数幂的乘法. 首先根据同底数幂的乘法法则,可得102m+3n=102m×103n,然后根据幂的乘方的运算方法,可得102m×103n=(10m)2×(10n)3,最后把10m=5,10n=2代入化简后的算式,求出102m+3n的值是多少即可.
【题型】填空题
【结束】
18【题目】计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-
 )2 016×161 008;
)2 016×161 008;
相关试题

