【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

参考答案:
【答案】(1)证明见解析;(2)当点O运动到AC的中点时,四边形AECF是矩形.理由见解析.
【解析】试题分析:(1)根据MN∥BC,CE平分∠ACB,CF平分∠ACD及等角对等边即可证得OE=OF;
(2)根据矩形的性质可知:对角线且互相平分,即AO=CO,OE=OF,故当点O运动到AC的中点时,四边形AECF是矩形.
(1)证明:∵MN∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠BCE=∠ACE=∠OEC,∠OCF=∠FCD=∠OFC,
∴OE=OC,OC=OF,
∴OE=OF.
(2)解:当O运动到AC中点时,四边形AECF是矩形,
∵AO=CO,OE=OF,
∴四边形AECF是平行四边形,
∵∠ECA+∠ACF=![]() ∠BCD,
∠BCD,
∴∠ECF=90°,
∴四边形AECF是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的解题过程:
计算:5÷(
 -2
-2 -2)×6.
-2)×6.解:5÷(
 -2
-2 -2)×6
-2)×6=5÷(-
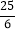 )×6…………①
)×6…………①=5÷(-25)…………②
=-
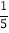 .…………③
.…………③回答:(1)上面的解题过程是从第________步开始出现错误的,错误的原因是___________________________________________________;
(2)请你给出正确的解题过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
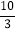 +(
+(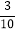 -
-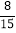 )÷(-
)÷(-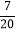 ); (2)-1-(1-
); (2)-1-(1- )÷3×|3-9|;
)÷3×|3-9|;(3)1
 +(2.4×
+(2.4× -
-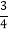 ×
× )÷2
)÷2 ; (4)(-3-1
; (4)(-3-1 )÷[3
)÷[3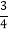 ÷(2-3
÷(2-3 )×1
)×1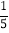 ].
]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C为线段AD上一点,B为CD的中点,且AD=10cm,BD=4cm;
(1)图中共有多少条线段?写出这些线段;
(2)求AC的长;
(3)若点E在直线AD上,且AE=3cm,求BE的长;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AC=BC=
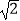 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ) 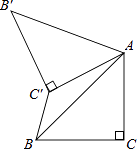
A.2﹣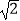
B.
C.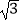 ﹣1
﹣1
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一副三角尺的直角顶点叠放在点C处,∠D=30°,∠B=45°,求:
(1)若∠DCE=35°,求∠ACB的度数;(2)若∠ACB=120°,求∠DCE的度数.
(3)猜想∠ACB和∠DCE的关系,并说明理由;

-
科目: 来源: 题型:
查看答案和解析>>【题目】据我国古代《周髀算经》记载,大约公元1120年,商高曾对周公说过一段话,其意思是将一根直尺折成一个直角,两端连接得一个直角三角形,如果勾是三,股是四,那么弦就等于五,后人概括为“勾三股四弦五”。
(1)观察:3,4,5; 5,12,13; 7,24,25……发现这些勾股数的勾都是奇数,且从3起就没有间断过。计算
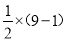 ,
, 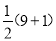 与
与 ,
,  并根据发现的规律,分别写出能表示7,24,25的股和弦的算式;
并根据发现的规律,分别写出能表示7,24,25的股和弦的算式;(2)根据(1)的规律,用n(n为奇数且n≥3)的代数式来表示所有这些勾股数的勾、股、弦,合理猜想它们之间的两种相等关系并对其一种猜想加以说明。
相关试题

