【题目】如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C
处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长
(![]() ≈1.73).
≈1.73).
参考答案:
【答案】简答:∵OA![]() ,
,
OB=OC=1500,
∴AB=![]() (m).
(m).
答:隧道AB的长约为635m.
【解析】
试题首先过点C作CO⊥AB,根据Rt△AOC求出OA的长度,根据Rt△CBO求出OB的长度,然后进行计算.
试题解析:如图,过点C作CO⊥直线AB,垂足为O,则CO="1500m"

∵BC∥OB ∴∠DCA=∠CAO=60°,∠DCB=∠CBO=45°
∴在Rt△CAO 中,OA=![]() =1500×
=1500×![]() =500
=500![]() m
m
在Rt△CBO 中,OB=1500×tan45°=1500m
∴AB=1500-500![]() ≈1500-865=635(m)
≈1500-865=635(m)
答:隧道AB的长约为635m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太繁,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.
因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=
 =5050.
=5050.(1)补全例题
 解题过程;
解题过程;(2)计算a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
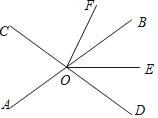
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)若|∠AOC﹣∠BOF|=α°,请直接写出∠AOC和∠BOF的度数.(用含的代数式表示)
-
科目: 来源: 题型:
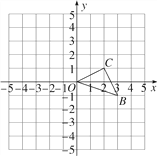
查看答案和解析>>【题目】如图,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以O点为位似中心,在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)如果△OBC内部一点M的坐标为(x,y),写出B,C,M的对应点B′,C′,M′的坐标.
-
科目: 来源: 题型:
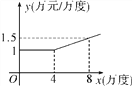
查看答案和解析>>【题目】某工厂在生产过程中每消耗1万度电可以产生产值5.5万元,电力公司规定,该工厂每月用电量不得超过16万度;月用电量不超过4万度时,单价都是1万元/万度;超过4万度时,超过部分电量单价将按用电量进行调整.电价y与月用电量x的函数关系可以用下图来表示(效益=产值-用电量×电价).
(1)求y与月用电量x之间的函数关系式,并写出自变量的取值范围;
(2)设工厂的月效益为z(万元),写出z与用电量x之间的函数关系式;
(3)求工厂最大月效益.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.

(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.
(1)若AB=10cm,则MN= cm;
(2)若AC=3cm,CP=1cm,求线段PN的长.

相关试题

