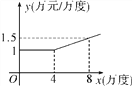
【题目】某工厂在生产过程中每消耗1万度电可以产生产值5.5万元,电力公司规定,该工厂每月用电量不得超过16万度;月用电量不超过4万度时,单价都是1万元/万度;超过4万度时,超过部分电量单价将按用电量进行调整.电价y与月用电量x的函数关系可以用下图来表示(效益=产值-用电量×电价).
(1)求y与月用电量x之间的函数关系式,并写出自变量的取值范围;
(2)设工厂的月效益为z(万元),写出z与用电量x之间的函数关系式;
(3)求工厂最大月效益.
参考答案:
【答案】(1);(2) z= ;(3)工厂最大月效益为54万元.
;(3)工厂最大月效益为54万元.
【解析】分析:(1)根据题意,电价y与用电量x的函数关系式是分段函数,当0≤x≤4时y=1,当4<x≤16时待定系数法可求得,(2)根据效益=产值-用电量×电价,分0≤x≤4,4<x≤16两种情况分别表示可得,(3)根据一次函数和二次函数性质结合自变量取值范围得到最大值,比较即可.
详解:(1)由题图知电价y与用电量x的函数关系式是分段函数.
当0≤x≤4时,y=1,
当4<x≤16时,函数是过点(4,1)和(8,1.5)的一次函数,
设一次函数为y=kx+b,
∴![]() ,
,
解得![]() ,
,
∴电价y与用电量x的函数关系为
y= ,
,
(2)月效益z与用电量x之间的函数关系式为:
z= ,
,
即z= ,
,
(3)当0≤x≤4时,z=![]() x,此时,z随着x的增大而增大,
x,此时,z随着x的增大而增大,
∴当x=4时,z取最大值为18.
当4<x≤16时,z=-![]() x2+
x2+![]() x-2=-
x-2=-![]() (x-22)2+
(x-22)2+![]() ,
,
∴当x≤22时,z随x的增大而增大,
∴当x=16时,z取最大值为54.
故当0≤x≤16时,z的最大值为54,
即工厂最大月效益为54万元.
-
科目: 来源: 题型:
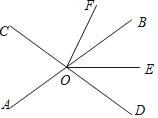
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)若|∠AOC﹣∠BOF|=α°,请直接写出∠AOC和∠BOF的度数.(用含的代数式表示)
-
科目: 来源: 题型:
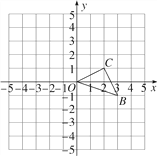
查看答案和解析>>【题目】如图,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以O点为位似中心,在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)如果△OBC内部一点M的坐标为(x,y),写出B,C,M的对应点B′,C′,M′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C
处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长
(
 ≈1.73).
≈1.73).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.

(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.
(1)若AB=10cm,则MN= cm;
(2)若AC=3cm,CP=1cm,求线段PN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
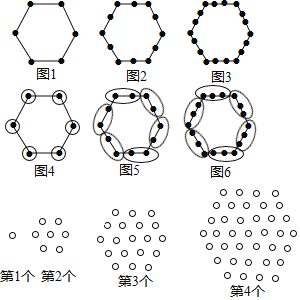
例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;所以容易求出图10、图n中黑点的个数分别是 、 .
请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题:
(1)第5个点阵中有 个圆圈;第n个点阵中有 个圆圈.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
相关试题

