【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,求证:∠DHO=∠DCO.

参考答案:
【答案】证明见解析
【解析】试题分析:根据菱形的对角线互相平分可得OD=OB,再根据直角三角形斜边上的中线等于斜边的一半可得OH=OB,然后根据等边对等角求出∠OHB=∠OBH,根据两直线平行,内错角相等求出∠OB
H=∠ODC,然后根据等角的余角相等证明即可.
试题解析:∵四边形ABCD是菱形,
∴OD=OB,∠COD=90°,
∵DH⊥AB,
∴OH=![]() BD=OB,
BD=OB,
∴∠OHB=∠OBH,
又∵AB∥CD,
∴∠OBH=∠ODC,
在Rt△COD中,∠ODC+∠DCO=90°,
在Rt△DHB中,∠DHO+∠OHB=90°,
∴∠DHO=∠DCO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个形如六边形的点阵,它的中心是一个点,算做第一层,第二层每边两个点,第三层每边三个点,以此类推.

(1)填写下表
层数
1
2
3
4
5
该层对应的点数
1
6
12
(2)写出第n层对应的点数(n≥2);
(3)如果某层一共有72个点,请你求出对应的层数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A. 7-2×(-
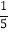 )=5×(-
)=5×(-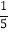 )=-1 B. -3÷7×
)=-1 B. -3÷7× =-3÷1=-3
=-3÷1=-3C. -32-(-3)2=-9-9=-18 D. 3×23-2×9=3×6-18=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE , 其中结论正确的个数为( )

A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④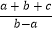 的最小值为3.
的最小值为3.
其中,正确结论的个数为( )
A.1个
B.2个
C.3个
D.4个
相关试题

