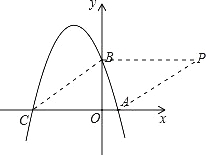
【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,
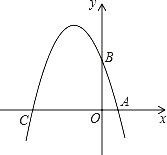
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.
参考答案:
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+3;(2)(5,3);(3)(1,0)或(﹣5,﹣
x+3;(2)(5,3);(3)(1,0)或(﹣5,﹣![]() );最大值为5.
);最大值为5.
【解析】试题分析:(1)设抛物线的解析式为y=ax2+bx+c,把A,B,C三点坐标代入求出a,b,c的值,即可确定出所求抛物线解析式;(2)在平面直角坐标系xOy中存在一点P,使得以点A、B、C、P为顶点的四边形为菱形,理由为:根据OA,OB,OC的长,利用勾股定理求出BC与AC的长相等,只有当BP与AC平行且相等时,四边形ACBP为菱形,可得出BP的长,由OB的长确定出P的纵坐标,确定出P坐标,当点P在第二、三象限时,以点A、B、C、P为顶点的四边形只能是平行四边形,不是菱形;(3)利用待定系数法确定出直线PA解析式,当点M与点P、A不在同一直线上时,根据三角形的三边关系|PM﹣AM|<PA,当点M与点P、A在同一直线上时,|PM﹣AM|=PA,当点M与点P、A在同一直线上时,|PM﹣AM|的值最大,即点M为直线PA与抛物线的交点,联立直线AP与抛物线解析式,求出当|PM﹣AM|的最大值时M坐标,确定出|PM﹣AM|的最大值即可.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c, ∵A(1,0)B(0,3)C(﹣4,0),
∴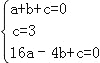 , 解得:a=﹣
, 解得:a=﹣![]() ,b=﹣
,b=﹣![]() ,c=3,
,c=3,
∴经过A、B、C三点的抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+3;
x+3;
(2)在平面直角坐标系xOy中存在一点P,使得以点A、B、C、P为顶点的四边形为菱形,理由为:
∵OB=3,OC=4,OA=1, ∴BC=AC=5, 当BP平行且等于AC时,四边形ACBP为菱形,
∴BP=AC=5,且点P到x轴的距离等于OB, ∴点P的坐标为(5,3),
当点P在第二、三象限时,以点A、B、C、P为顶点的四边形只能是平行四边形,不是菱形,
则当点P的坐标为(5,3)时,以点A、B、C、P为顶点的四边形为菱形;
(3)设直线PA的解析式为y=kx+b(k≠0), ∵A(1,0),P(5,3),
∴![]() , 解得:k=
, 解得:k=![]() ,b=﹣
,b=﹣![]() , ∴直线PA的解析式为y=
, ∴直线PA的解析式为y=![]() x﹣
x﹣![]() ,
,
当点M与点P、A不在同一直线上时,根据三角形的三边关系|PM﹣AM|<PA,
当点M与点P、A在同一直线上时,|PM﹣AM|=PA,
∴当点M与点P、A在同一直线上时,|PM﹣AM|的值最大,即点M为直线PA与抛物线的交点,
解方程组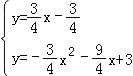 ,得
,得![]() 或
或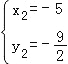 ,
,
∴点M的坐标为(1,0)或(﹣5,﹣![]() )时,|PM﹣AM|的值最大,此时|PM﹣AM|的最大值为5.
)时,|PM﹣AM|的值最大,此时|PM﹣AM|的最大值为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图直角坐标系中直线 AB 与 x 轴正半轴、y 轴正半轴交于 A,B 两点,已知 B(0,4),∠BAO=30°,P,Q 分别是线段 OB,AB 上的两个动点,P 从 O 出发以每秒 3 个单位长度的速度向终点 B 运动,Q 从 B 出发以每秒 8 个单位长度的速度向终点 A 运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为 t(秒).
(1)求线段 AB 的长,及点 A 的坐标;
(2)t 为何值时,△BPQ 的面积为
 ;
;(3)若 C 为 OA 的中点,连接 QC,QP,以 QC,QP 为邻边作平行四边形 PQCD,
①t 为何值时,点 D 恰好落在坐标轴上;
②是否存在时间 t 使 x 轴恰好将平行四边形 PQCD 的面积分成 1∶3 的两部分,若存在,直接写出 t 的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】天水市某企业接到一批粽子生产任务,按要求在19天内完成,约定这批粽子的出厂价为每只4元,为按时完成任务,该企业招收了新工人,设新工人李红第x天生产的粽子数量为y只,y与x满足如下关系:
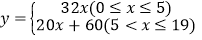 .
.(1)李红第几天生产的粽子数量为260只?
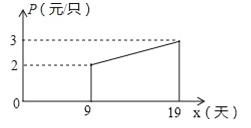
(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画,若李红第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价﹣成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究规律:我们有可以直接应用的结论:若两条直线平行,那么在一条直线上任取一点,无论这点在直线的什么位置,这点到另一条直线的距离均相等.例如:如图1,两直线
 ∥
∥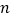 ,两点
,两点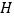 ,
,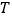 在
在 上,
上, ⊥
⊥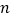 于
于 ,
, ⊥
⊥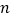 于
于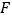 ,则
,则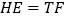 .
.如图2,已知直线
 ∥
∥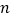 ,
, ,
, 为直线
为直线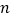 上的两点,
上的两点, .
. 为直线
为直线 上的两点.
上的两点.(1)请写出图中面积相等的各对三角形: .
(2)如果
 ,
, ,
, 为三个定点,点
为三个定点,点 在
在 上移动,那么无论
上移动,那么无论 点移动到任何位置,总有: 与
点移动到任何位置,总有: 与 的面积相等;理由是: .
的面积相等;理由是: .
解决问题:
如图3,五边形
 是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图4所示的形状,但承包土地与开垦荒地的分界小路(图4中折线
是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图4所示的形状,但承包土地与开垦荒地的分界小路(图4中折线 )还保留着,张大爷想过点
)还保留着,张大爷想过点 修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多.请你用以上的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)
修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多.请你用以上的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)(1)写出设计方案,并在图4中画出相应的图形;
(2)说明方案设计理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:满足(1)各边互不相等且均为整数;(2)最短边上的高与最长边上的高的比值为整数k。这样的三角形称为比高三角形,其中k叫做比高系数。根据规定解答下列问题:
(1)周长为13的比高三角形的比高系数k= ;
(2)比高三角形△ABC三边与它的比高系数k之间满足BC-AC=AC-AB=k2,求△ABC的周长的最小值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )

A. 20 B. 24 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ADC=130°,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,交对边于F、E,且∠ABF=∠AED,过E作EH⊥AD交AD于H。
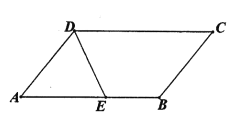
(1)在图中作出线段BF和EH(不要求尺规作图);
(2)求∠AEH的大小。
小亮同学根据条件进行推理计算,得出结论,请你在括号内注明理由。
证明:∵BF、DE分别平分∠ABC与∠ADC,(已知)
∴∠ABF=
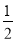 ∠ABC,∠CDE=
∠ABC,∠CDE=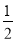 ∠ADC。( )
∠ADC。( )∵∠ABC=∠ADC,(已知)
∴∠ABF=∠CDE。(等式的性质)
∵∠ABF=∠AED,(已知)
∴∠CDE=∠AED。( )
∴AB∥CD。( )
∵∠ADC=130°(已知)
∴∠A=180°-∠ADC=50°(两直线平行,同旁内角互补)
∵EH⊥AD于H(已知)
∴∠EHA=90°(垂直的定义)
∴在Rt△AEH中,∠AEH=90°-∠A( )=40°。
相关试题

