【题目】如图,∠ADC=130°,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,交对边于F、E,且∠ABF=∠AED,过E作EH⊥AD交AD于H。
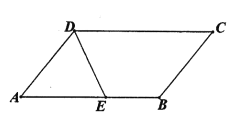
(1)在图中作出线段BF和EH(不要求尺规作图);
(2)求∠AEH的大小。
小亮同学根据条件进行推理计算,得出结论,请你在括号内注明理由。
证明:∵BF、DE分别平分∠ABC与∠ADC,(已知)
∴∠ABF=![]() ∠ABC,∠CDE=
∠ABC,∠CDE=![]() ∠ADC。( )
∠ADC。( )
∵∠ABC=∠ADC,(已知)
∴∠ABF=∠CDE。(等式的性质)
∵∠ABF=∠AED,(已知)
∴∠CDE=∠AED。( )
∴AB∥CD。( )
∵∠ADC=130°(已知)
∴∠A=180°-∠ADC=50°(两直线平行,同旁内角互补)
∵EH⊥AD于H(已知)
∴∠EHA=90°(垂直的定义)
∴在Rt△AEH中,∠AEH=90°-∠A( )=40°。
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)根据题意作图即可;
(2)根据证明过程写出相应的理由即可.
作∠ABC的平分线BF, 过E作EH⊥AD交AD于H,如图所示
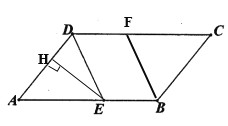
(2) 角平分线性质 等式的性质 内错角相等,两直线平行 在直角三角形中,两锐角互余
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,
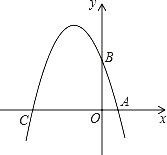
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:满足(1)各边互不相等且均为整数;(2)最短边上的高与最长边上的高的比值为整数k。这样的三角形称为比高三角形,其中k叫做比高系数。根据规定解答下列问题:
(1)周长为13的比高三角形的比高系数k= ;
(2)比高三角形△ABC三边与它的比高系数k之间满足BC-AC=AC-AB=k2,求△ABC的周长的最小值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )

A. 20 B. 24 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时 间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
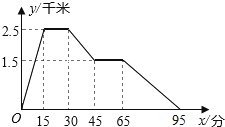
A. 体育场离张强家2.5千米
B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店1.千米
D. 张强从早餐店回家的平均速度是3千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=
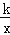 (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( )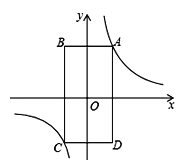
A. 一直增大 B. 一直减小 C. 先增大后减小 D. 先减小后增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=
 (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
A.b=2a+k B.a=b+k C.a>b>0 D.a>k>0
相关试题

