【题目】如图直角坐标系中直线 AB 与 x 轴正半轴、y 轴正半轴交于 A,B 两点,已知 B(0,4),∠BAO=30°,P,Q 分别是线段 OB,AB 上的两个动点,P 从 O 出发以每秒 3 个单位长度的速度向终点 B 运动,Q 从 B 出发以每秒 8 个单位长度的速度向终点 A 运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为 t(秒).
(1)求线段 AB 的长,及点 A 的坐标;
(2)t 为何值时,△BPQ 的面积为![]() ;
;
(3)若 C 为 OA 的中点,连接 QC,QP,以 QC,QP 为邻边作平行四边形 PQCD,
①t 为何值时,点 D 恰好落在坐标轴上;
②是否存在时间 t 使 x 轴恰好将平行四边形 PQCD 的面积分成 1∶3 的两部分,若存在,直接写出 t 的值.

参考答案:
【答案】![]() ; (2)1或
; (2)1或![]() ;(3)①
;(3)①![]() 或
或![]() ;②
;②![]() .
.
【解析】
由30°角的性质求出AB的长,由勾股定理求出OA的长,进而可求出点A的坐标;
(2)由运动知,OP=3t,BQ=8t,BP=43t,过点Q作QH⊥OB于H,由勾股定理求出HQ的长,然后利用三角形的面积公式求解即可;
(3)①当点D在y轴上时,QC∥PD,利用三角形的中位线求解即可;当点D在x轴上时,PQ∥AD,利用sin∠BQP=![]() 求解即可;
求解即可;
②如图 ,连接PC,过点Q作QH⊥OB于H,过点D作DF⊥OA于F,由平行四边形的性质知S△CPQ=S△PCD,由x轴恰好将平行四边形PQCD的面积分成1:3的两部分,可得S△PCE=S△DCE,可证DF=OP=3t,然后证明延长DF,PQ相交于M,延长HQ交DM于N,然后证明△CDF≌△QPH,可得PH=DF=3t,利用4t+3t+3t=4即可求出t的值.
解:(1)∵B(0,4),
∴OB=4,
在Rt△AOB中,∠BAO=30°,
∴AB=2OB=8,BC=![]() OB=4
OB=4![]() ,
,
∴A(4![]() ,0).
,0).
(2)如图1,
由运动知,OP=3t,BQ=8t,
∴BP=43t,
过点Q作QH⊥OB于H,
∴HQ=4![]() t,
t,
∵△BPQ的面积为2![]() ,
,
∴![]() (43t)×4
(43t)×4![]() t
t
=2![]() ,
,
∴t=1或t=![]() .
.

(3)①当点D在y轴上时,QC∥PD,

∵C是OA中点,
∴BQ=![]() AB=4,
AB=4,
∴8t=4,
∴t=![]() ,
,
当点D在x轴上时,

∵PQ∥AD,
∴∠BPQ=90°,
∴sin∠BQP=![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
②如图 ,连接PC,过点Q作QH⊥OB于H,过点D作DF⊥OA于F,
∵四边形CDPQ是平行四边形,
∴S△CPQ=S△PCD,
∵x轴恰好将平行四边形PQCD的面积分成1:3的两部分,
∴S△PCE=S△DCE,
∴点E是DP的中点,
易知,DF=OP=3t,
延长DF,PQ相交于M,延长HQ交DM于N,
∵CD∥PQ,
∴∠M=∠CDF,∠M=∠HPQ,
∴∠CDF=∠HPQ,
∵CD=PQ,
∴△CDF≌△QPH,
∴PH=DF=3t,
∵BH=![]() BQ=4t,
BQ=4t,
∴4t+3t+3t=4,
∴t=![]() .
.
-
科目: 来源: 题型:
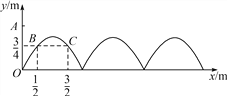
查看答案和解析>>【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C两点到地面的距离均为
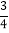 m,到墙边OA的距离分别为
m,到墙边OA的距离分别为 m,
m, m.
m.(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10 m,则最多可以连续绘制几个这样的拋物线型图案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】你知道古代数学家怎样解一元二次方程吗?以x2﹣2x﹣3=0为例,大致过程如下:第一步:将原方程变形为x2﹣2x=3,即x(x﹣2)=3.
第二步:构造一个长为x,宽为(x﹣2)的长方形,长比宽大2,且面积为3,如图所示.
第三步:用四个这样的长方形围成一个大正方形,中间是一个小正方形,如图所示.
第四步:计算大正方形面积用x表示为 .长方形面积为常数 .小正方形面积为常数 .
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,得方程 ,两边开方可求得:x1=3,x2=﹣1.
(1)第四步中横线上应填入 ; ; ; .
(2)请参考古人的思考过程,画出示意图,写出步骤,解方程x2﹣x﹣1=0.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠DEF:∠EFH=3:2,∠1=∠B,∠2+∠3=180°,求∠DEF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】天水市某企业接到一批粽子生产任务,按要求在19天内完成,约定这批粽子的出厂价为每只4元,为按时完成任务,该企业招收了新工人,设新工人李红第x天生产的粽子数量为y只,y与x满足如下关系:
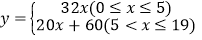 .
.(1)李红第几天生产的粽子数量为260只?
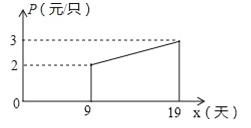
(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画,若李红第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价﹣成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究规律:我们有可以直接应用的结论:若两条直线平行,那么在一条直线上任取一点,无论这点在直线的什么位置,这点到另一条直线的距离均相等.例如:如图1,两直线
 ∥
∥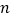 ,两点
,两点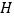 ,
,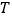 在
在 上,
上, ⊥
⊥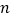 于
于 ,
, ⊥
⊥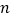 于
于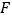 ,则
,则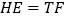 .
.如图2,已知直线
 ∥
∥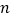 ,
, ,
, 为直线
为直线 上的两点,
上的两点, .
. 为直线
为直线 上的两点.
上的两点.(1)请写出图中面积相等的各对三角形: .
(2)如果
 ,
, ,
, 为三个定点,点
为三个定点,点 在
在 上移动,那么无论
上移动,那么无论 点移动到任何位置,总有: 与
点移动到任何位置,总有: 与 的面积相等;理由是: .
的面积相等;理由是: .
解决问题:
如图3,五边形
 是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图4所示的形状,但承包土地与开垦荒地的分界小路(图4中折线
是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图4所示的形状,但承包土地与开垦荒地的分界小路(图4中折线 )还保留着,张大爷想过点
)还保留着,张大爷想过点 修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多.请你用以上的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)
修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多.请你用以上的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)(1)写出设计方案,并在图4中画出相应的图形;
(2)说明方案设计理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,
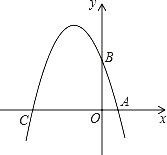
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.
相关试题

