【题目】某车间一周内计划每天生产100辆电动车,由于工人实行轮休,每天上班人数不一定相等,实际每天生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | ﹣5 | +5 | ﹣5 | +5 | +10 | ﹣10 | ﹣15 |
(1)本周三生产了多少辆电动车?
(2)本周总产量与计划总生产量相比,是增加多少辆?还是减少多少辆?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
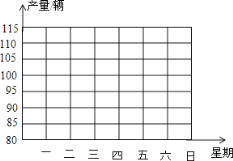
(4)请你用折线图画出电动车产量的变化情况.
参考答案:
【答案】(1)95辆;(2)减少15辆;(3)25辆 ;(4)见解析
【解析】
(1)根据表格列出算式,计算即可得到结果;
(2)表格中的数据相加得到结果,即可做出判断;
(3)找出产量最多与最少的,相减即可得到结果;
(4)根据表格中的数据先求出本周每天的产量,再画出折线统计图即可.
(1)本周三生产的电动车数量为:100+(-5)=95(辆);
(2)根据题意得:
(-5)+5+(-5)+5+10+(-10)+(-15)=-15,
则本周总产量与计划总生产量相比,减少了15辆;
(3)产量最多的一天比产量最少的一天多生产(+10)-(-15)=25(辆),
则产量最多的一天比产量最少的一天多生产了25辆;
(4)本周每天的产量为:
星期一:100+(-5)=95(辆),星期二:100+(+5)=105(辆),
星期四:100+(+5)=105(辆),星期五:100+(+10)=110(辆),
星期六:100+(-10)=90(辆),星期日:100+(-15)=85(辆),
折线图如下:
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形,对角线AC,BD相交于点O.
(1)如图1,点P是正方形ABCD外一点,连接OP,以OP为一边,作正方形OPMN,且边ON与边BC相交,连接AP,BN.
①依题意补全图1;
②判断AP与BN的数量关系及位置关系,写出结论并加以证明;
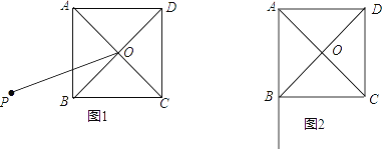
(2)点P在AB延长线上,且∠APO=30°,连接OP,以OP为一边,作正方形OPMN,且边ON与BC的延长线恰交于点N,连接CM,若AB=2,求CM的长(不必写出计算结果,简述求CM长的过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.60元,由公路运输,每千克需运费0.30元,另需补助600元
(1)设该公司运输的这批牛奶为x千克,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1、y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500千克牛奶,则选用哪种运输方式所需费用较少?
-
科目: 来源: 题型:
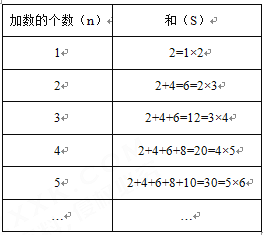
查看答案和解析>>【题目】从2开始,连续的偶数相加,它的和的情况如下表:
(1)当n个最小的连续偶数相加时,它们的和s与n之间的关系式为s= (用含n的式子表示)
(2)并由此计算:
①2+4+6+8+…+50;
②52+54+56+…+100.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的单位长度为1,A、B两点表示的数是互为相反数;
(1)点A表示的数是 ,点B表示的数是
(2)数轴上一个动点P先向左移动2个单位长度,再向右移动5个单位到达点M,若点M表示的数是1,则点P所表示的数是
(3)(背景知识)数轴上,点A、B表示的数分别记为a、b,当点P在A、B之间,且到A、B的距离相等,即PA=PB,则点P表示的数可记为
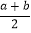 .
.若点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度向右运动,点P以1个单位长度/秒的速度从O点向右运动.当三点同时运动时,不妨设运动时间为t秒,(t>0)
①点P表示的数为 ;点A表示的数为 ;点B表示的数为 .(用含t的式子表示)
②当t为何值时,点A、点B、点P三点之间恰好有一个点到其他两个点的距离相等?

-
科目: 来源: 题型:
查看答案和解析>>【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB⊥AC,以点A为圆心,AB为半径的圆交BC于点E.
(1)求证:DE为⊙O的切线;
(2)如果BE=4,CE=2,求DE的值.
相关试题

