搜索
【题目】如图，一位篮球运动员跳起投篮，球沿抛物线y=﹣ 
x2+3.5运行，然后准确落入篮框内．已知篮框的中心离地面的距离为3.05米．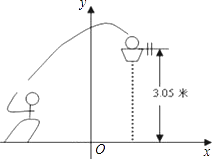 
（1）球在空中运行的最大高度为多少米？
（2）如果该运动员跳投时，球出手离地面的高度为2.25米，请问他距离篮框中心的水平距离是多少？
参考答案：
【答案】
（1）解：因为抛物线y=﹣ 
x2+3.5的顶点坐标为（0，3.5）
所以球在空中运行的最大高度为3.5米；
（2）解：当y=3.05时，3.05=﹣ x2+3.5，
解得：x=±1.5
又因为x＞0
所以x=1.5
当y=2.25时，
x=±2.5
又因为x＜0
所以x=﹣2.5，
由|1.5|+|﹣2.5|=1.5+2.5=4米，
故运动员距离篮框中心水平距离为4米
【解析】（1）最大高度应是抛物线顶点的纵坐标的值；（2）根据所建坐标系，水平距离是蓝框中心到Y轴的距离+球出手点到y轴的距离，即两点横坐标的绝对值的和．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解，完成下列各题
定义：已知A、B、C 为数轴上任意三点，若点C 到A 的距离是它到点B 的距离的2 倍，则称点C 是[A，B]的2 倍点．例如：如图1，点C 是[A，B]的2 倍点，点D 不是[A，B]的2 倍点，但点D 是[B，A]的2 倍点，根据这个定义解决下面问题：
（1）在图1 中，点A 是 的2倍点，点B是 的2 倍点；（选用A、B、C、D 表示，不能添加其他字母）；
（2）如图2，M、N 为数轴上两点，点M 表示的数是﹣2，点N 表示的数是4，若点E是[M，N]的2倍点，则点E 表示的数是 ；
（3）若P、Q 为数轴上两点，点P在点Q的左侧，且PQ=m，一动点H从点Q 出发，以每秒2个单位长度的速度沿数轴向左运动，设运动时间为t 秒，求当t 为何值时，点H 恰好是P和Q两点的2倍点？（用含m 的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数的图象经过点（0，﹣3），顶点坐标为（﹣1，﹣4），
（1）求这个二次函数的解析式；
（2）求图象与x轴交点A、B两点的坐标；
（3）图象与y轴交点为点C，求三角形ABC的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】我国古代数学名著《算法统宗》中，有一道“群羊逐草”的问题，大意是：牧童甲在草原上放羊，乙牵着一只羊来，并问甲：“你的羊群有100只吗？”甲答：“如果在这群羊里加上同样的一群，再加上半群，四分之一群，再加上你的一只，就是100只．”问牧童甲赶着多少只羊？若设这群羊有x只，则下列方程中，正确的是（ ）
A. （1+
+
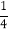）x=100+1 B. x+x+x+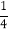x=100﹣1 C. （1++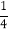）x=100﹣1 D. x+x+x+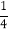x=100+1 -
科目： 来源： 题型：
查看答案和解析>>【题目】某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量y（本）与每本纪念册的售价x（元）之间满足一次函数关系：当销售单价为22元时，销售量为36本；当销售单价为24元时，销售量为32本．
（1）请直接写出y与x的函数关系式；
（2）当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？
（3）设该文具店每周销售这种纪念册所获得的利润为w元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知正比例函数y＝kx的图象经过点(3，－6)．
(1)求这个函数的解析式；
(2)画出这个函数图象；
(3)判断点A(4，－2)、点B(－1.5，3)是否在这个函数图象上；
(4)图象上有两点C(x1，y1)，D(x2，y2)，如果x1＞x2，比较y1，y2的大小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点M为直线AB上一动点，
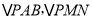都是等边三角形，连接BN 
求证： 
；
分别写出点M在如图2和图3所示位置时，线段AB、BM、BN三者之间的数量关系
不需证明
；
如图4，当
时，证明： 
．
相关试题
