搜索
【题目】已知二次函数的图象经过点（0，﹣3），顶点坐标为（﹣1，﹣4），
（1）求这个二次函数的解析式；
（2）求图象与x轴交点A、B两点的坐标；
（3）图象与y轴交点为点C，求三角形ABC的面积．
参考答案：
【答案】
（1）解：设抛物线的解析式为y=a（x+1）2﹣4，
把点（0，﹣3）代入得a﹣4=﹣3，解得a=1，
所以函数解析式y=（x+1）2﹣4或y=x2+2x﹣3
（2）解：当y=0时，x2+2x﹣3=0，解得x1=1，x2=﹣3，
所以A（﹣3，0），B（1，0）
（3）解：C（0，﹣3），
△ABC的面积= 
×（1+3）×3=6
【解析】（1）设顶点式y=a（x+1）2﹣4，然后把点（0，﹣3）代入求出a即可得到抛物线解析式；（2）通过解方程可得到A点和B点坐标；（3）先写出C点坐标，然后根据三角形面积公式计算．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，△ABC的位置如图所示（每个小方格都是边长为1个单位长度的正方形）．
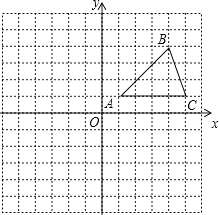
（1）将△ABC沿x轴方向向左平移6个单位，画出平移后得到的△A1B1C1；
（2）将△ABC绕着点A顺时针旋转90°，画出旋转后得到的△AB2C2 ， 并直接写出点B2、C2的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3＋2
＝(1＋
)2，善于思考的小明进行了以下探索：设a＋b
＝(m＋n
)2(其中a、b、m、n均为正整数)，则有a＋b
＝m2＋2n2＋2mn
，∴a＝m2＋2n2，b＝2mn.这样小明就找到了一种把a＋b
的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：
（1）当a、b、m、n均为正整数时，若a＋b
＝(m＋n
)2，用含m、n的式子分别表示a、b，得：a＝ , b＝ . （2）利用所探索的结论，找一组正整数a、b、m、n填空： + = ( + )2；(答案不唯一)
（3）若a＋4
＝(m＋n
)2 ,且a、m、n均为正整数,求a的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，是一台自动测温仪记录的图象，它反映了我市冬季某天气温T随时间t变化而变化的关系，观察图象得到下列信息，其中错误的是（ ）
A. 凌晨4时气温最低为－3℃
B. 14时气温最高为8℃
C. 从0时至14时，气温随时间增长而上升
D. 从14时至24时，气温随时间增长而下降
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一位篮球运动员跳起投篮，球沿抛物线y=﹣
x2+3.5运行，然后准确落入篮框内．已知篮框的中心离地面的距离为3.05米． 
（1）球在空中运行的最大高度为多少米？
（2）如果该运动员跳投时，球出手离地面的高度为2.25米，请问他距离篮框中心的水平距离是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】某校对七年级(5)班男生进行100 m短跑测试，以12.5 s为测试达标标准，超过的秒数用正数表示，不足的秒数用负数表示，某小组10名男生的成绩如下表所示：(单位：s)
＋0.25
－1
－0.27
0
－0.56
－0.33
0
0.6
＋0.45
－0.14
(1)求出这10名男生100 m短跑测试的达标率；
(2)这10名男生短跑共用时多少秒？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量y（本）与每本纪念册的售价x（元）之间满足一次函数关系：当销售单价为22元时，销售量为36本；当销售单价为24元时，销售量为32本．
（1）请直接写出y与x的函数关系式；
（2）当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？
（3）设该文具店每周销售这种纪念册所获得的利润为w元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？
相关试题
