【题目】填写推理理由
如图,已知AD⊥BC于D,EF⊥BC于F,AD平分∠BAC.将∠E=∠1的过程填写完整.
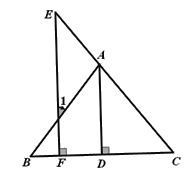
解:解:∵AD⊥BC, EF⊥BC( 已知 )
∴∠ADC=∠EFC= 90°( 垂直的意义 )
∴AD//EF
∴∠1= ()
∠E= ()
又∵AD平分∠BAC(已知 )
∴ =
∴∠1=∠E.
参考答案:
【答案】见解析
【解析】
试题由AD垂直于BC,EF垂直于BC,得到一对同位角相等,利用同位角相等两直线平行得到AD与EF平行,利用两直线平行内错角相等得到一对角相等,再由AD为角平分线得到一对角相等,等量代换即可得证.
试题解析:∵AD⊥BC,EF⊥BC(已知)
∴∠ADC=∠EFC=90°(垂直的意义)
∴AD∥EF
∴∠1=∠BAD(两直线平行,内错角相等)
∴∠E=∠CAD(两直线平行,同位角相等)
又∵AD平分∠BAC(已知)
∴∠BAD=∠CAD
∴∠1=∠E.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是A.B两所学校艺术节期间收到的各类艺术作品情况的统计图:


A学校 B学校
(1)从图中你能否看出哪所学校收到的水粉画作品的数量多?为什么?
(2)已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺木作品的总数分别是多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=BC,将△ABC绕顶点B逆时针方向旋转
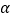 度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.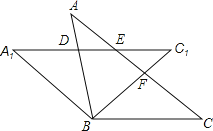
(1)若∠ABC=
 ,∠DBF=
,∠DBF=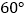 ,则
,则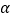 =______°;
=______°;(2)求证:△BCF≌△BA1D;
(3)连接DF,当∠DBF=
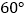 时,判定△DBF的形状并说明理由.
时,判定△DBF的形状并说明理由. -
科目: 来源: 题型:
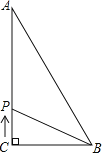
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.
(1)当t为何值时,CP把△ABC的周长分成相等的两部分.
(2)当t为何值时,CP把△ABC的面积分成相等的两部分,并求出此时CP的长;(说明:直角三角形斜边上的中线等于斜边的一半)
(3)当t为何值时,△BCP为等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图像如图所示,当气球内气压大于120kPa时,气球将爆炸,为了安全起见,气球内的体积应( )

A. 小于1.25m3 B. 大于1.25m3 C. 不小于0.8m3 D. 大于0.8m
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小长度为G1、G2的“密距”.例如,如上图,
 ,
, ,
, ,则点A与射线OC之间的“密距”为
,则点A与射线OC之间的“密距”为 ,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线
,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线 之间的“密距”为
之间的“密距”为 ,则k值为( )
,则k值为( )
A. k=4 B. k=-4 C. k=6 D. k=-6
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生课余活动情况,某校对参加绘画、书法、舞蹈、乐器这四个课外兴趣小组的人员分布情况进行抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下面的问题:

(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中书法部分的圆心角的度数;
(3)如果该校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的20名学生,估计每个兴趣小组至少需要准备多少名教师?
相关试题

