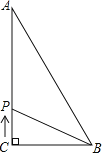
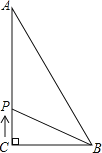
【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.
(1)当t为何值时,CP把△ABC的周长分成相等的两部分.
(2)当t为何值时,CP把△ABC的面积分成相等的两部分,并求出此时CP的长;(说明:直角三角形斜边上的中线等于斜边的一半)
(3)当t为何值时,△BCP为等腰三角形?
参考答案:
【答案】(1)6秒;(2)5cm;(3)当t=3秒或5.4秒或6秒或6.5秒时,△BCP为等腰三角形.
【解析】分析:(1)先由勾股定理求出△ABC的斜边AB=10cm,则△ABC的周长为24cm,所以当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,再根据时间=路程÷速度即可求解;
(2)根据中线的性质可知,点P在AB中点时,CP把△ABC的面积分成相等的两部分,进而求解即可;
(3)△BCP为等腰三角形时,分三种情况进行讨论:①CP=CB;②BC=BP;③PB=PC.
详解:(1)△ABC中,∵∠C=Rt∠,AC=8cm,BC=6cm,
∴AB=10cm,
∴△ABC的周长=8+6+10=24cm,
∴当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,
∴t=12÷2=6(秒);
(2)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时CA+AP=8+5=13(cm),∴t=13÷2=6.5(秒),
∴CP=![]() AB=
AB=![]() ×10=5cm;
×10=5cm;
(3)△BCP为等腰三角形时,分三种情况:
①如果CP=CB,那么点P在AC上,CP=6cm,此时t=6÷2=3(秒);
如果CP=CB,那么点P在AB上,CP=6cm,此时t=5.4(秒)
(点P还可以在AB上,此时,作AB边上的高CD,利用等面积法求得CD=4.8,再利用勾股定理求得DP=3.6,所以BP=7.2,AP=2.8,所以t=(8+2.8)÷2=5.4(秒))
②如果BC=BP,那么点P在AB上,BP=6cm,CA+AP=8+10-6=12(cm),此时t=12÷2=6(秒);
③如果PB=PC,那么点P在BC的垂直平分线与AB的交点处,即在AB的中点,此时CA+AP=8+5=13(cm),
t=13÷2=6.5(秒);
综上可知,当t=3秒或5.4秒或6秒或6.5秒时,△BCP为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过正五边形ABCDE的顶点D作直线l∥AB,则∠1的度数是 .
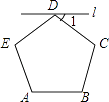
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是A.B两所学校艺术节期间收到的各类艺术作品情况的统计图:


A学校 B学校
(1)从图中你能否看出哪所学校收到的水粉画作品的数量多?为什么?
(2)已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺木作品的总数分别是多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=BC,将△ABC绕顶点B逆时针方向旋转
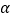 度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.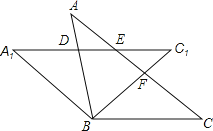
(1)若∠ABC=
 ,∠DBF=
,∠DBF=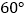 ,则
,则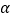 =______°;
=______°;(2)求证:△BCF≌△BA1D;
(3)连接DF,当∠DBF=
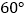 时,判定△DBF的形状并说明理由.
时,判定△DBF的形状并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】填写推理理由
如图,已知AD⊥BC于D,EF⊥BC于F,AD平分∠BAC.将∠E=∠1的过程填写完整.
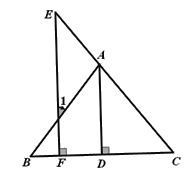
解:解:∵AD⊥BC, EF⊥BC( 已知 )
∴∠ADC=∠EFC= 90°( 垂直的意义 )
∴AD//EF
∴∠1= ()
∠E= ()
又∵AD平分∠BAC(已知 )
∴ =
∴∠1=∠E.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图像如图所示,当气球内气压大于120kPa时,气球将爆炸,为了安全起见,气球内的体积应( )

A. 小于1.25m3 B. 大于1.25m3 C. 不小于0.8m3 D. 大于0.8m
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小长度为G1、G2的“密距”.例如,如上图,
 ,
, ,
, ,则点A与射线OC之间的“密距”为
,则点A与射线OC之间的“密距”为 ,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线
,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线 之间的“密距”为
之间的“密距”为 ,则k值为( )
,则k值为( )
A. k=4 B. k=-4 C. k=6 D. k=-6
相关试题

