【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.求证:

(1)AB∥CD;
(2)∠2+∠3=90°.
参考答案:
【答案】证明见解析
【解析】
试题分析:(1)首先根据角平分线的定义可得∠ABD=2∠1,∠BDC=2∠2,根据等量代换可得∠ABD+∠BDC=2∠1+2∠2=2(∠1+∠2),进而得到∠ABD+∠BDC=180°,然后根据同旁内角互补两直线平行可得答案;
(2)先根据三角形内角和定理得出∠BED=90°,再根据三角形外角的性质得出∠EDF+∠3=90°,由角平分线的定义可知∠2=∠EDF,代入得到∠2+∠3=90°.
证明:(1)∵DE平分∠BDC(已知),
∴∠ABD=2∠1( 角平分线的性质).
∵BE平分∠ABD(已知),
∴∠BDC=2∠2(角的平分线的定义).
∴∠ABD+∠BDC=2∠1+2∠2=2(∠1+∠2)( 等量代换).
∵∠1+∠2=90°(已知),
∴∠ABD+∠BDC=180°( 等式的性质).
∴AB∥CD( 同旁内角互补两直线平行).
(2)∵∠1+∠2=90°,
∴∠BED=180°﹣(∠1+∠2)=90°,
∴∠BED=∠EDF+∠3=90°,
∵∠2=∠EDF,
∴∠2+∠3=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠A=145°,∠D=75°.
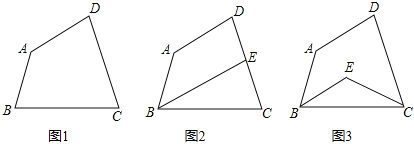
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a3a2正确的是( )
A. a B. a5 C. a6 D. a9
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=﹣
 x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以-3和7为根且二次项系数为1的一元二次方程是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次消防演习中,消防员架起一架25米长的云梯,如图斜靠在一面墙上,梯子底端离墙7米.
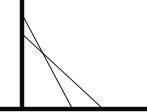
(1)求这个梯子的顶端距地面有多高?
(2)如果消防员接到命令,要求梯子的顶端下降4米(云梯长度不变),那么云梯的底部在水平方向应滑动多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】分别有下列几组数据:①6、8、10 ②12、13、5 ③ 17、8 、15 ④4、11、9其中能构成直角三形的有( )
A. 4组 B. 3组 C. 2组 D. 1组
相关试题

