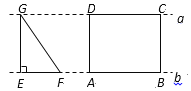
【题目】如图,点![]() 、
、![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 、
、![]() 、
、![]() 、
、![]() 在直线
在直线![]() 上,若
上,若![]() ,
,![]() 从如图所示的位置出发,沿直线
从如图所示的位置出发,沿直线![]() 向右匀速运动,直到
向右匀速运动,直到![]() 与
与![]() 重合时停止运动.在运动过程中,
重合时停止运动.在运动过程中,![]() 与矩形
与矩形![]() (
(![]() )重合部分的面积
)重合部分的面积![]() 随时间
随时间![]() 变化的图象大致是( )
变化的图象大致是( )
A. 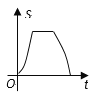 B.
B. 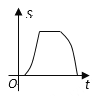 C.
C. 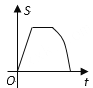 D.
D. 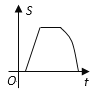
参考答案:
【答案】B
【解析】根据题意可得:
F,A重合之前没有重叠面积,
F,A重叠之后到E与A重叠前,设AE=a, EF被重叠部分的长度为(ta),则重叠部分面积为![]() ,∴是二次函数图象;
,∴是二次函数图象;
③△EFG完全进入且F与B重合之前,重叠部分的面积是三角形的面积,不变,
④F与B重合之后,重叠部分的面积等于S=S△EFG12(ta)2tan∠EFG,符合二次函数图象,直至最后重叠部分的面积为0.
综上所述,只有B选项图形符合。
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要想使一个六边形活动支架ABCDEF稳固且不变形,至少需要增加_____根木条才能固定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果多项式x2+mx+16是一个完全平方式,则m的值是( )
A.±4B.4C.8D.±8
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求,用四舍五入法取下列各数的近似数:1.4149≈(精确到千分位)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.

(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.

请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式A=2x2-xy+my-8,B=-nx2+xy+y+7,A-2B中不含有x2项和y项,求nm+mn的值.
相关试题

