【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.

请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
参考答案:
【答案】(1)a=300;(2)108°;(3)12~23岁的人数为400万
【解析】试题分析:(1)根据30-35岁的人数和所占的百分比求调查的人数;
(2)从调查的总人数中减去已知的三组的人数,即可得到12-17岁的人数,据此补全条形统计图;
(3)先计算18-23岁的人数占调查总人数的百分比,再计算这一组所对应的圆心角的度数;
(4)先计算调查中12﹣23岁的人数所占的百分比,再求网瘾人数约为2000万中的12﹣23岁的人数.
试题解析:解:(1)结合条形统计图和扇形统计图可知,30-35岁的人数为330人,所占的百分比为22%,所以调查的总人数为330÷22%=1500人.
故答案为:1500 ;
(2)1500-450-420-330=300人.
补全的条形统计图如图:

(3)18-23岁这一组所对应的圆心角的度数为360×![]() =108°.
=108°.
故答案为:108° ;
(4)(300+450)÷1500=50%,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求,用四舍五入法取下列各数的近似数:1.4149≈(精确到千分位)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
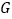 、
、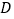 、
、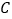 在直线
在直线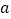 上,点
上,点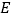 、
、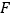 、
、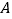 、
、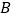 在直线
在直线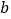 上,若
上,若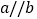 ,
,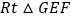 从如图所示的位置出发,沿直线
从如图所示的位置出发,沿直线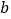 向右匀速运动,直到
向右匀速运动,直到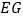 与
与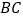 重合时停止运动.在运动过程中,
重合时停止运动.在运动过程中,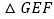 与矩形
与矩形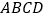 (
( )重合部分的面积
)重合部分的面积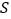 随时间
随时间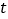 变化的图象大致是( )
变化的图象大致是( )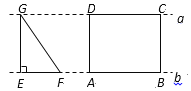
A.
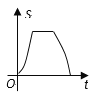 B.
B. 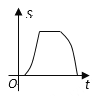 C.
C. 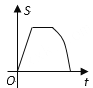 D.
D. 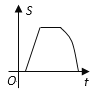
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.

(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式A=2x2-xy+my-8,B=-nx2+xy+y+7,A-2B中不含有x2项和y项,求nm+mn的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明的身份证号码是321281199202030630,他出生日期是年月日.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形、菱形、正方形都一定具有的性质是( )
A.对角线垂直B.对角线互相平分
C.四个角都是直角D.对角线相等
相关试题

