【题目】某汽车销售公司4月份销售某厂家的汽车,在一定范围内每部汽车的进价与销售量有如下关系;若当月仅售出1辆汽车,则该部汽车的进价为25万元,每多售出1辆,所有售出的汽车的进价均降低0.2万元/辆,月底厂家根据销售量一次性返利给销售公司,销售量在10辆以内(含10辆),每辆返利0.6万元;销售量在10辆以上,每辆返利1.2万元.
(1)若该公司当月售出3辆汽车,则每辆汽车的进价为________万元;
(2)若该公司当月售出5辆汽车,且每辆汽车售价为![]() 元,则该销售公司该月盈利________万元(用含
元,则该销售公司该月盈利________万元(用含![]() 的代数式表示).
的代数式表示).
(3)如果汽车的售价为25.6万元/辆,该公司计划当月盈利16.8万元,那么需要售出多少辆汽车?(盈利销售利润+返利)
参考答案:
【答案】(1)24.6;(2)(5m-121);(3)7
【解析】
(1)根据题意每多售出1辆,所有售出的汽车的进价均降低0.2万元/辆,即可得出当月售出3辆汽车时,每辆汽车的进价;
(2)先表示出当月售出5辆汽车时每辆汽车的进价,再根据利润=售价-进价即可求得该月盈利;
(3)首先表示出每辆汽车的销售利润,再利用当0≤x≤10,当x>10时,分别得出答案.
解:(1)∵当月仅售出1辆汽车,则该辆汽车的进价为25万元,每多售出1辆,所有售出的汽车的进价均降低0.1万元/辆,
∴该公司当月售出3辆汽车,则每辆汽车的进价为25-2×0.2=24.6万元;
故答案为:24.6;
(2) ∵当月售出5辆汽车,
∴每辆汽车的进价为25-4×0.2=24.2万元,
∴该月盈利为5(m-24.2)=5m-121,
故答案为:(5m-121);
(2)设需要售出x辆汽车,由题意可知,每辆汽车的销售利润为:
25.6-[25-0.2(x-1)]=(0.2x+0.4)(万元),
当0≤x≤10,根据题意,得x(0.2x+0.4)+0.6x=16.8,
整理,得x2+5x-84=0,
解这个方程,得x1=-12(不合题意,舍去),x2=7,
当x>10时,根据题意,得x(0.2x+0.4)+1.2x=16.8,
整理,得x2+8x-84=0,
解这个方程,得x1=-14(不合题意,舍去),x2=6,
因为6<10,所以x2=6舍去.
答:需要售出7辆汽车.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电信检修小组从A地出发,在东西向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下。(单位:km)
第一次
第二次
第三次
第四次
第五次
第六次
第七次
-3
+7
-9
+8
+6
-5
-4
(1)求收工时距A地多远?
(2)在第几次纪录时距A地最远?
(3)若每km耗油0.2升,问共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】六(2)班同学准备春游,某品牌牛奶每盒200毫升,售价2元.
(1)在甲商店购买,买5盒送一盒;在乙商场购买,九折优惠.全班42人,要给每位同学准备一瓶这样的牛奶,该去哪家商场购买比较合算?为什么?
(2)商店提供装牛奶的是一个长方体纸箱,下面是它的展开图,请算出这个长方体纸箱的表面积.(黏贴处不算,单位:分米)

-
科目: 来源: 题型:
查看答案和解析>>【题目】底边长为6厘米,高为9厘米的等腰三角形20个,迭放如图:
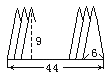
每两个等腰三角形有等距离的间隔,底边迭合在一起的长度是44厘米.回答下列问题:
(1)两个三角形的间隔距离;
(2)三个三角形重迭(两次)部分的面积之和;
(3)只有两个三角形重迭(一次)部分的面积之和;
(4)迭到一起的总面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①内错角相等;②对顶角相等;③三角形的一个外角大于任何一个内角;④若三条线段
 、
、 、
、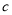 满足
满足 ,则三条线段
,则三条线段 、
、 、
、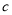 一定能组成三角形其中正确的个数是( )
一定能组成三角形其中正确的个数是( )A. 1个B. 2个C. 3个D. 4个.
-
科目: 来源: 题型:
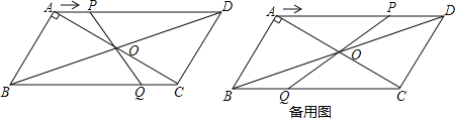
查看答案和解析>>【题目】 如图,在ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动速度为lcm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),当t=4时,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,并回答下列问题:
小明遇到这样一个问题,如图,在
 中,
中, 分别交
分别交 于点
于点 ,交
,交 于点
于点 .已知
.已知 ,求
,求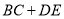 的值.
的值.小明发现,过点
 作
作 ,交
,交 的延长线于点
的延长线于点 ,构造
,构造 ,经过推理和计算能够使问题得到解决(如图)
,经过推理和计算能够使问题得到解决(如图)
请你回答:
(1)证明:
 ;
;(2)求出
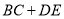 的值;
的值;(3)参考小明思考问题的方法,解决问题;
如图,已知
 和矩形
和矩形 与
与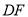 交于点
交于点 .求
.求 的度数.
的度数.
相关试题

