【题目】认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图l,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90![]() +
+![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴∠1=![]() ∠ABC, ∠2=
∠ABC, ∠2=![]() ∠ACB
∠ACB
∴∠l+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180
(180![]() -∠A)= 90
-∠A)= 90![]() -
-![]() ∠A
∠A
∴∠BOC=180![]() -(∠1+∠2) =180
-(∠1+∠2) =180![]() -(90
-(90![]() -
-![]() ∠A)=90
∠A)=90![]() +
+![]() ∠A
∠A
(1)探究2;如图2中,O是![]() ∠ABC与外角
∠ABC与外角![]() ∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(2)探究3:如图3中, O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(直接写出结论)
(3)拓展:如图4,在四边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)

参考答案:
【答案】(1)探究2结论:∠BOC=![]() ;(2)探究3:结论∠BOC=90°-
;(2)探究3:结论∠BOC=90°-![]() ;(3)拓展:结论
;(3)拓展:结论![]()
【解析】
(1)根据角平分线的定义可得∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义可得∠2=
∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义可得∠2=![]() ∠ACD=
∠ACD=![]() (∠A+∠ABC),∠BOC=∠2-∠1,然后整理即可得解;
(∠A+∠ABC),∠BOC=∠2-∠1,然后整理即可得解;
(2)根据三角形的外角性质以及角平分线的定义表示出∠OBC和∠OCB,再根据三角形的内角和定理解答;
(3)同(1)的求解思路.
(1)探究2结论:∠BOC=![]() ∠A.
∠A.
理由如下:如图,
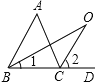
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACD,
∠ACD,
又∵∠ACD是△ABC的一个外角,
∴∠2=![]() ∠ACD=
∠ACD=![]() (∠A+∠ABC)=
(∠A+∠ABC)=![]() ∠A+∠1,
∠A+∠1,
∵∠2是△BOC的一个外角,
∴∠BOC=∠2-∠1=![]() ∠A+∠1-∠1=
∠A+∠1-∠1=![]() ∠A,
∠A,
即∠BOC=![]() ∠A;
∠A;
(2)由三角形的外角性质和角平分线的定义,∠OBC=![]() (∠A+∠ACB),∠OCB=
(∠A+∠ACB),∠OCB=![]() (∠A+∠ABC),
(∠A+∠ABC),
在△BOC中,∠BOC=180°-∠OBC-∠OCB=180°-![]() (∠A+∠ACB)-
(∠A+∠ACB)-![]() (∠A+∠ABC),
(∠A+∠ABC),
=180°-![]() (∠A+∠ACB+∠A+∠ABC),
(∠A+∠ACB+∠A+∠ABC),
=180°-![]() (180°+∠A),
(180°+∠A),
=90°-![]() ∠A;
∠A;
故答案为:∠BOC=90°-![]() ∠A.
∠A.
(3)∠OBC+∠OCB=![]() (360°-∠A-∠D),
(360°-∠A-∠D),
在△BOC中,∠BOC=180°-![]() (360°-∠A-∠B)=
(360°-∠A-∠B)=![]() (∠A+∠D).
(∠A+∠D).
故答案为:∠BOC=![]() (∠A+∠D).
(∠A+∠D).
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备举行社团活动,需要向商家购买A,B两种型号的文化衫50件,己知一件A型号文化衫的售价比一件B型号文化衫的售价贵9元,用200元恰好可以买到2件A型号文化衫和S件B型号文化杉.
(1)求A、B两种型号的文化衫每件的价格分别为多少元?
(2)如果用于购买A、B两种型号文化杉的金额不少于1500元但不超过1530元,请体求出所有的购买方案?
(3)试问在(2)的条件下,学校采用哪种购买方案花钱最少?最少是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在ABCD中,点E,F在对角线BD上,且BE=DF,
求证:(1)AE=CF;(2)四边形AECF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(
 ,1)在反比例函数y=
,1)在反比例函数y=  的图象上.
的图象上.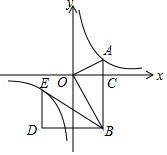
(1)求k的值;
(2)若将△BOA绕点B按逆时针方向旋转60°,得到△BDE,判断点E是否在该反比例函数的图象上,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一小题计分.
①若单项式﹣xmyn+4 与 5x2y 是同类项,则 nm 的值为____.
②实施西部大开发战略是党中央的重大决策,我国国土面积约为960 万平方千米,而我国西部地区的面积占我国国土面积的
 ,用科学记数法表示我国西部地区的面积约为_____平方千米.
,用科学记数法表示我国西部地区的面积约为_____平方千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
相关试题

