【题目】甲、乙两人分别从相距100km的A、B两地同时出发相向而行,并以各自的速度匀速行驶.甲出发2h后到达B地立即按原路返回,返回时速度提高了30km/h,回到A地后在A地休息等乙,乙在出发5h后到达A地.(友情提醒:可以借助用线段图分析题目)
(1)乙的速度是_______![]() ,甲从A地到B地的速度是_______
,甲从A地到B地的速度是_______![]() ,甲在出发_______小时到达A地.
,甲在出发_______小时到达A地.
(2)出发多长时间两人首次相遇?
(3)出发多长时间时,两人相距30千米?
参考答案:
【答案】(1)20km/h, 50 km/h, 3.25小时;
(2)出发![]() 小时两人相遇;
小时两人相遇;
(3)出发1或![]() 或
或![]() 或
或![]() 或3.5小时,两人相距30千米.
或3.5小时,两人相距30千米.
【解析】
(1)根据甲乙两地相距100km,甲用时2h,乙用时5h,即可得出答案;
(2)根据甲乙两人共走了100km,列方程即可得出答案;
(3)分情况进行讨论:①两人第一次相遇之前相距30km,②两人第一次相遇之后相距30km,③两人第二次相遇之前相距30km,④两人第二次相遇之后相距30km,⑤甲回到A地之后乙返回并距离A地30km.
解:(1)乙的速度是100÷5=20km/h,甲从A地到B地的速度是100÷2=50 km/h,甲在出发2+100÷(50+30)=3.25小时到达A地;
(2)设出发x小时两人相遇,由题意得
50x+20x=100
解得:x=![]() ,
,
答:出发![]() 小时两人相遇.
小时两人相遇.
(3)设出发a小时,两人相距30千米,由题意得
50a+20a=100﹣30或50a+20a=100+30或20a﹣(50+30)(a﹣2)=30或(50+30)(a﹣2)﹣20a=30或20(a﹣65÷20)=100﹣65﹣30,
解得:a=1或a=![]() 或a=
或a=![]() 或a=
或a=![]() 或a=3.5
或a=3.5
答:出发1或![]() 或
或![]() 或
或![]() 或3.5小时,两人相距30千米.
或3.5小时,两人相距30千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现了解情况如下:甲、乙两家商店出售两种同样品牌的笔记本和钢笔.笔记本定价为每本20元,钢笔每支定价5元,经洽谈后,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.七年级需笔记本20本,钢笔若干支(不小于20支).问:
(1)如果购买钢笔
 (
( 不小于20)支,则在甲店购买需付款 ______ 元,在乙店购买需付款 _______________ 元.(用x的代数式表示)
不小于20)支,则在甲店购买需付款 ______ 元,在乙店购买需付款 _______________ 元.(用x的代数式表示)(2)当购买钢笔多少支时,在两店购买付款一样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在
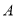 处测得灯塔
处测得灯塔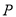 在北偏东
在北偏东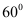 方向上,继续航行1小时到达
方向上,继续航行1小时到达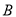 处,此时测得灯塔
处,此时测得灯塔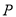 在北偏东
在北偏东 方向上.
方向上.(1)求
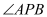 的度数;
的度数;(2)已知在灯塔
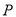 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?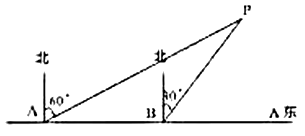
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线:y=a(x-m)2-a(x-m)(a、m为常数,且a≠0).
(1)求证:不论a与m为何值,该抛物线与x轴总有两个公共点;
(2)设该抛物线与x轴相交于A、B两点,则线段AB的长度是否与a、m的大小有关系?若无关系,求出它的长度;若有关系,请说明理由;
(3)在(2)的条件下,若抛物线的顶点为C,当△ABC的面积等于1时,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过
 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=
 ,AH=
,AH=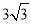 ,求EM的值.
,求EM的值.
-
科目: 来源: 题型:
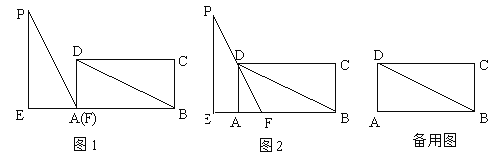
查看答案和解析>>【题目】如图1,在矩形ABCD中,DB=6,AD=3,在Rt△PEF中,∠PEF=90°,EF=3,PF=6,△PEF(点F和点A重合)的边EF和矩形的边AB在同一直线上.现将Rt△PEF从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,
解答下列问题:
(1)如图1,连接PD,填空:∠PFD= ,四边形PEAD的面积是 ;
(2)如图2,当PF经过点D时,求 △PEF运动时间t的值;
(3)在运动的过程中,设△PEF与△ABD重叠部分面积为S,请求出S与t的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
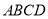 的对角线
的对角线 和
和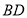 相交于点
相交于点 ,正方形
,正方形 的边
的边 交
交 于点
于点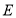 ,
, 交
交 于点
于点 .
.
(1)求证:
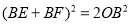 ;
;(2)如果正方形
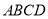 的边长为
的边长为 ,那么正方形
,那么正方形 绕
绕 点转动的过程中,与正方形
点转动的过程中,与正方形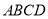 重叠部分的面积始终等于__________.(用含
重叠部分的面积始终等于__________.(用含 的代数式表示)
的代数式表示)
相关试题

